What open-source projects have I contributed to Github in 2020?

Today is the last day of 2020, which means it is time to have my 2020 Github Rewind! Last year I've had 1,775 contributions on Github and I got 4,104 contributions as of today. You can see my Github profile [here](https://github.com/wingkwong).  Let's go through what I've worked on one by one in an arbitrary order. ## vote4hk/warsinhk  [warsinhk](https://github.com/vote4hk/warsinhk) is a static website for [covid19.vote4.hk](covid19.vote4.hk). I've developed some components such as alert message boxes, datepicker, share buttons and etc, integreated react-i18next, did some bug fixing and revised the documentation. ## aws/aws-sam-cli [aws-sam-cli](https://github.com/aws/aws-sam-cli) is a CLI tool to build, test, debug, and deploy Serverless applications using AWS SAM.  I've worked on a bug ticket with Jacob who is a senior software engineer at AWS. The bug was about the attribute ``Command.ScriptLocation`` not being updated for ``Glue::Job`` when running ``sam build`` because dot notations were not supported. At the beginning, my implementation was a bit complicated and Jacob suggested to use ``jmespath`` to handle the querying for nested attributes in JSON instead. The pull request was merged after 2-month discussion. ## wingkwong/hk-address-parser [hk-address-parser](https://github.com/wingkwong/hk-address-parser) is an unofficial library for [Hong Kong Address Parser](https://g0vhk-io.github.io/HKAddressParser/#/), designed for Python applications. The usage is pretty simple. ``` from hk_address_parser import AddressParser # Single Query address = AddressParser.parse( "Eaton Hotel, 380 Nathan Road, Jordan") # Batch Query addresses = AddressParser.parse( [ "九龍觀塘海濱道 181號 9樓", "九龍長沙灣道 303號長沙灣政府合署 12樓", "九龍啟德協調道 3號工業貿易大樓 5樓", "香港中環統一碼頭道 38號海港政府大樓 7樓", "香港北角渣華道 333號北角政府合署 12樓1210-11室", "九龍旺角聯運街 30號旺角政府合署 5樓 503室", "九龍觀塘鯉魚門道 12號東九龍政府合署 7樓", "九龍深水埗南昌邨南昌社區中心高座 3樓", "九龍黃大仙龍翔道 138號龍翔辦公大樓 8樓 801室", "新界沙田上禾輋路 1號沙田政府合署 7樓 708-714室", "新界大埔墟鄉事會街 8號大埔綜合大樓 4樓", "新界荃灣大河道 60號雅麗珊社區中心 3樓", "新界屯門震寰路 16號大興政府合署 2樓 201室", "新界元朗橋樂坊 2號元朗政府合署暨大橋街市 12樓" ] ``` Then you can call the [methods](https://github.com/wingkwong/hk-address-parser#methods) to get the corresponding info. ## cli/cli  [cli](https://github.com/cli/cli) is GitHub’s official command line tool written in Go. I've worked on the command ``gh gist create`` which is used to create a new Github gist with given contents. The feature has been released. For the usage, please check out the official documentation [here](https://cli.github.com/manuala/gh_gist_create). ## aws/copilot-cli  [copilot-cli](https://github.com/aws/copilot-cli) is a tool for developers to build, release and operate production ready containerized applications on Amazon ECS and AWS Fargate. I was responsible for a few bug fixing tickets and a feature adding an optional env flag to the command ``app delete`` with test cases. ## wingkwong/k8sgen  [k8sgen](https://github.com/wingkwong/k8sgen), written in Go, is an utility which is designed to guide users to build their Kubernetes resources in an interactive CLI. At that time I was learning k8s and drilling down into the details of its internal designs. It was an experimental project. ```bash k8sgen jumpstart _ ___ | | _( _ ) ___ __ _ ___ _ __ | |/ / _ \/ __|/ _ |/ _ | |_ \ | | (_) \__ | (_| | __| | | | |_|\_\___/|___/\__, |\___|_| |_| |___/ ? What kind of object you want to create? [Use arrows to move, type to filter] ClusterRole ClusterRoleBinding Configmap > Deployment Job Namespace PodDisruptionBudget PriorityClass Quota Role RoleBinding Secret Service ServiceAccount ? What deployment you want to name? my-deployment ? What image you want to name to run? busybox ? Please select an output format yaml json > yaml ? What directory you want to save? /home/wingkwong/deployment.yaml ``` Result: ``` apiVersion: apps/v1 kind: Deployment metadata: creationTimestamp: null labels: app: my-deployment name: my-deployment spec: replicas: 1 selector: matchLabels: app: my-deployment strategy: {} template: metadata: creationTimestamp: null labels: app: my-deployment spec: containers: - image: busybox name: busybox resources: {} status: {} ``` ## cortexlabs/cortex  [Cortex](https://github.com/cortexlabs/cortex) is an open source platform for large-scale inference workloads. I added a feature to support ``.cortexignore`` file to exclude files/directories from cortex project zip and also updated AWS resource metadata. ## wingkwong/react-quiz-component [react-quiz-component](https://github.com/wingkwong/react-quiz-component) is a ReactJS component allowing users to attempt a quiz. I've added some new features and worked on some bug fixing tickets. Currently it got 10K+ downloads in NPM. ## alexellis/k3sup  [k3sup](https://github.com/alexellis/k3sup) is a light-weight utility to get from zero to KUBECONFIG with k3s on any local or remote VM. All you need is ssh access and the k3sup binary to get kubectl access immediately. I've made a pull request with the changes to add ``app info`` sub-command to show post-install instructions for an app and the app homepage link, so that users don't have to unnecessarily install again to see them, which was the only way till now to see post install instructions. The changes were implemented for nginx-ingress, cert-manager, metrics-server, tiller, linkerd, cron-connector, kafka-connector, minio, postgresql, kubernetes-dashboard, istio, and crossplane commands. ## inlets/inlets & inlets/inletsctl  [inlets](https://github.com/inlets/inlets) is a Cloud Native Tunnel written in Go and [inletsctl](https://github.com/inlets/inletsctl) creates inlets tunnel servers in the cloud. The same bug was found in both repository. When running ``get.sh``, the program will fail if the target folder contains a space. Therefore I made the same fix to both repository. The fix was simple enough - just added several double quotes. ## My Self-Learning Playgrounds I learn something new by doing when I feel bored. Here's the list. - [aws-playground](https://github.com/wingkwong/aws-playground) - [azure-playground](https://github.com/wingkwong/azure-playground) - [gcp-playground](https://github.com/wingkwong/gcp-playground) - [qsharp-playground](https://github.com/wingkwong/qsharp-playground) - [nlp-playground](https://github.com/wingkwong/nlp-playground) - [deno-playground](https://github.com/wingkwong/deno-playground) - [gRPC-playground](https://github.com/wingkwong/gRPC-playground) - [argocd-playground](https://github.com/wingkwong/argocd-playground) - [skaffold-playground](https://github.com/wingkwong/skaffold-playground) - [traefik-playground](https://github.com/wingkwong/traefik-playground) - [lxd-playground](https://github.com/wingkwong/lxd-playground) ## wingkwong/competitive-programming [competitive-programming](https://github.com/wingkwong/competitive-programming) contains CP solutions (mostly written in C++) from different OJs and contest sites with explanations. I believe most of the commits come from this repository as I've solved quite a lot of problems this year.  Competitive programming is a mind sport for programmers to solve mathematical or logical problems. I started my CP journey in 2014 and I had a chance to participant in ACM-HK Collegiate Programming Contest in 2015. I took a long break since then. Most of the people practice lots of CP problems just to get into FANNG companies but I only treat it as a hobby. ## Conclusion In 2020, I mainly worked on CLI projects in Go, practiced 1000+ CP problems in C++, and learned cloud native stuff. In the next year, I believe I'll focus on advanced algorithms. Probably I'll try to use different programming languages to solve the CP problems to sharpen my programming skills.

Finding Longest Palindrome in O(n) Using Manacher's Algorithm

You can practice the problem [here](https://cses.fi/problemset/task/1111/). Given a string, your task is to determine the longest palindromic substring of the string. For example, the longest palindrome in aybabtu is bab. A palindrome here is a string which reads the same backward as forward. We can use functions like ``reverse`` to check if the given string is a palindrome or not. ```cpp bool is_palindrome(string s) { string t = s; reverse(t.begin(), t.end()); return s == t; } ``` Or we can use two pointers. ```cpp bool is_palindrome(string s) { int l = 0, r = (int) s.size() - 1; while(l < r) { if(s[l] != s[r]) return false; else l++, r--; } return true; } ``` The first approach is brute force. ```cpp int n = (int) s.size(), start = 0, mx_len = 1; REP(i, n) { REP(j, i) { int ok = 1; REP(k, (j - i + 1) / 2) { if(s[i + k] != s[j - k]) ok = 0; } if(ok && (j - i + 1) > mx_len) { start = i; mx_len = j - i + 1; } } } OUT(s.substr(start, mx_len)); ``` However, the time complexity for this solution is O(n ^ 3) because we need three nested loops to find the longest palindromic substring. It only works when n is really small. The second approach is dynamic programming. The time complexity can be further reduced to O(n ^ 2). We use dp[i][j] to indicate if s[i] .. s[j] is a palindrome or not. Let's think about the transitions. 1. If i == j, that means s[i] == s[j], a single character is a palindrome. Example: a. 2. If i + 1 == j and s[i] == s[j], then s[i] .. s[j] is a palindrome. Example: aa. 3. If dp[i + 1][j - 1] and s[i] == s[j], then s[i] .. s[j] is a palindrome. Example: abba. As we can see, dp[i + 1][j] needs to be calculated before d[i][j]. Therefore, we iterate i from n - 1 to 0 and j from i + 1 to n. ```cpp int n = (int) s.size(); vvi dp(n, vi(n, 0)); string ans; int start = 0, len = 1; REP(i, n) dp[i][i] = 1; FORD(i, n - 1, 0) { FOR(j, i + 1, n) { if(s[i] == s[j]) { if(i + 1 == j || dp[i + 1][j - 1]) { dp[i][j] = 1; if(len < j - i + 1) { start = i; len = j - i + 1; } } } } } OUT(s.substr(start, len)); ``` With dynamic programming, the time cplexity and auxiliary space are O(n ^ 2). However, we can solve the problem in linear time using Manacher's algorithm. As a palindrome has a symmetric property at the center position, it could help us to reduce some unnecessary computations. If there is a palindrome of length N centered at position P, we can avoid the comparisions after position P as we already calculated longest palindromic substring at position before P. However, an even palidrome has two centers, which makes the calculate a little bit different than the one calculating for an odd palindrome. Here's the implementation in C++. ```cpp string manacher(string s) { int n = (int) s.size(); // d1[i]: the number of palindromes accordingly with odd lengths with centers in the position i. // d2[i]: the number of palindromes accordingly with even lengths with centers in the position i. vector d1(n), d2(n); int l1 = 0, r1 = -1, l2 = 0, r2 = -1, mx_len = 0, start = 0; for (int i = 0; i < n; i++) { // ---------------------- // calculate d1[i] // ---------------------- int k = (i > r1) ? 1 : min(d1[l1 + r1 - i], r1 - i + 1); while (0 <= i - k && i + k < n && s[i - k] == s[i + k]) k++; d1[i] = k--; if (i + k > r1) l1 = i - k, r1 = i + k; if(d1[i] * 2 > mx_len) start = i - k, mx_len = d1[i] * 2 - 1; // ---------------------- // calculate d2[i] // ---------------------- k = (i > r2) ? 0 : min(d2[l2 + r2 - i + 1], r2 - i + 1); while (0 <= i - k - 1 && i + k < n && s[i - k - 1] == s[i + k]) k++; d2[i] = k--; if (i + k > r2) l2 = i - k - 1, r2 = i + k; if(d2[i] * 2 > mx_len) start = i - k - 1, mx_len = d2[i] * 2; } // return the longest palindrome return s.substr(start, mx_len); } ``` If you want to count how many palindromic substrings in the given string, simply sum d1[i] and d2[i] where i = 0 .. n - 1. ```cpp int cnt = 0; for(int i = 0; i < n; i++) cnt += d1[i] + d2[i]; ``` This problem can also be solved using fast LCA in O(n) or String Hashing O(nlogn). These methods will not be discussed in this post. You can find the whole solution [here](https://github.com/wingkwong/competitive-programming/blob/09531f2fbfbf03393ba3e744cb77858134463e29/cses/string-algorithms/1111-longest-palindrome.cpp).

BOJ 1890 - 점프

# 문제 N×N 게임판에 수가 적혀져 있다. 이 게임의 목표는 가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 규칙에 맞게 점프를 해서 가는 것이다. 각 칸에 적혀있는 수는 현재 칸에서 갈 수 있는 거리를 의미한다. 반드시 오른쪽이나 아래쪽으로만 이동해야 한다. 0은 더 이상 진행을 막는 종착점이며, 항상 현재 칸에 적혀있는 수만큼 오른쪽이나 아래로 가야 한다. 한 번 점프를 할 때, 방향을 바꾸면 안 된다. 즉, 한 칸에서 오른쪽으로 점프를 하거나, 아래로 점프를 하는 두 경우만 존재한다. 가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 규칙에 맞게 이동할 수 있는 경로의 개수를 구하는 프로그램을 작성하시오. # 입력 첫째 줄에 게임 판의 크기 N (4 ≤ N ≤ 100)이 주어진다. 그 다음 N개 줄에는 각 칸에 적혀져 있는 수가 N개씩 주어진다. 칸에 적혀있는 수는 0보다 크거나 같고, 9보다 작거나 같은 정수이며, 가장 오른쪽 아래 칸에는 항상 0이 주어진다. # 출력 가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 문제의 규칙에 맞게 갈 수 있는 경로의 개수를 출력한다. 경로의 개수는 263-1보다 작거나 같다. # 예제 입력 ``` 4 2 3 3 1 1 2 1 3 1 2 3 1 3 1 1 0 ``` # 예제 출력 ``` 3 ``` # 정답 ```cpp const int mxN = 105; ll n, dp[mxN][mxN], vis[mxN][mxN], g[mxN][mxN]; int dx[2] = {1, 0}, dy[2] = {0, 1}; ll dfs(int x, int y) { vis[x][y] = 1; if(x == n - 1 && y == n - 1) return 1; if(dp[x][y] || g[x][y] == 0) return dp[x][y]; for(int i = 0; i < 2; i++) { int next_x = x + g[x][y] * dx[i]; int next_y = y + g[x][y] * dy[i]; if(next_x < 0 || next_x >= n || next_y < 0 || next_y >= n || vis[next_x][next_y]) continue; dp[x][y] += dfs(next_x, next_y); vis[next_x][next_y] = 0; } return dp[x][y]; } void solve() { cin >> n; REP(i, n) REP(j, n) cin >> g[i][j]; OUT(dfs(0, 0)); } int main() { FAST_INP; solve(); return 0; } ```

AtCoder - ABC185C. Duodecim Ferra

You can practice the problem Duodecim Ferra [here](https://atcoder.jp/contests/abc185/tasks/abc185_c). ## Problem Statement There is an iron bar of length ``L`` lying east-west. We will cut this bar at 11 positions to divide it into 12 bars. Here, each of the 12 resulting bars must have a positive integer length. Find the number of ways to do this division. Two ways to do the division are considered different if and only if there is a position cut in only one of those ways. Under the constraints of this problem, it can be proved that the answer is less than 2^63. ## Solutions This problem can be solved using Stars and Bars Theorem. Given the lenght ``L``, we have a Diophantine equation ``x[0] + x[1] + ... + x[11] = L`` where x[i] are the lengths of the bars after the division. We need to select 11 positions out of ``L - 1`` positions. For example, if ``L`` is 14, we will have the following possible points to cut. ``` 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 ``` Therefore, the answer is ``` C(n, r) = C(L - 1, r - 1) = C(14 - 1, 12 - 1) = C(13, 11) = 78 ``` We can solve it in O(r) time complexity and O(1) space complexity . nCr can be written as ``` (n)! / (r)!( / (n - r)! = (n * (n - 1) * (n - 2) * ... * 1 ) / (r * (r - 1) * (r - 2) * ... * 1) / ((n - r) * (n - r - 1) * (n - r - 2) * ... * 1) = n * (n - 1) * (n - 2) * ... * (n - (r - 1)) / (r * (r - 1) * (r - 2) * ... * 1) ``` ```cpp // AC - 3 ms void solve() { ll L; cin >> L; ll ans = 1; FOR(i, 1, 12) { ans *= L - i; // n * (n - 1) * (n - 2) * ... * (n - (r - 1)) ans /= i; // r * (r - 1) * (r - 2) * ... * 1 } OUT(ans); } ``` We can turn it to a template for similar problems ```cpp template< typename T > T comb(int64_t N, int64_t K) { if(K < 0 || N < K) return 0; T ret = 1; for(T i = 1; i <= K; ++i) { ret *= N--; ret /= i; } return ret; } // AC - 7 ms void solve() { ll L; cin >> L; OUT(comb<ll>(L - 1, 11)); } ``` We can also use dynamic programming to solve this problem. The recursive formula is ``` C(n, r) = C(n - 1, r - 1) + C(n - 1, r) ``` For ``r == 0`` and ``n == r``, the result would be 1. ```cpp // AC - 10 ms const int mxN = 205; ll c[mxN][mxN]; void solve() { ll L; cin >> L; REP(i, l) { c[i][0] = c[i][i] = 1; FOR(j, 1, i) { c[i][j] = c[i - 1][j - 1] + c[i - 1][j]; } } OUT(c[L - 1][11]); } ```

TLX - TROC17A. Firework Festival

You can practice the question [here](https://tlx.toki.id/contests/troc-17/problems/A). Given two arrays A and B, each of size N. Determine whether the sum of A[i]^B[i] for all 1 <= i <= N, is odd or even. Display the output 0 if the sum is even, or 1 if the sum is odd. Input Format ``` N A[1] A[2] ... A[N] B[1] B[2] ... B[N] ``` Sample Input ``` 5 2 4 6 8 2 1 2 3 4 5 ``` Sample Output ``` 0 ``` Constraints ``` 1 <= N <= 100 1 <= A[i], B[i] <= 100 ``` Usually for Problem A, most of the solutions are brute-force. However, if we take the edge case 100, A[0] ^ B[0] + A[1] ^ B[1] + ... + A[99] ^ B[99] where A[i] and B[i] are 100, the overall result would occur overflow. We can notice that this problem is all about parity. The exponent B[i] of A[i] does not change the parity of A[i] ^ B[i]. Hence, we can conclude that ``` even ^ odd -> even even ^ even -> even odd ^ even -> odd odd ^ even -> odd ``` and we know that ``` even + even -> even odd + odd -> even even + odd -> odd ``` Therefore, we can simply sum all the values and check if it is even or odd. ```cpp int main() { int n; cin >> n; vi a(n), b(n); READ(a); READ(b); int sum = 0; REP(i, n) sum += a[i]; OUT((sum & 1)); return 0; } ```

Finding all occurrences of a pattern in a given string in linear time using Z Algorithm

Given a string S and a pattern P, find all occurences of P in S. Supposing the length of S is m and that of P is n, we can find the answer using Z Algorithm in linear time. First, we need to construct a Z array where Z[i] is the length of longest common prefix between S and the suffix starting from S[i]. If Z[i] = 0, it means that S[0] != S[i] and the first element of Z is generally not defined. ``` vector<int> z_function(string s) { int n = (int) s.length(); vector<int> z(n); for (int i = 1, l = 0, r = 0; i < n; ++i) { if (i <= r) z[i] = min (r - i + 1, z[i - l]); while (i + z[i] < n && s[z[i]] == s[i + z[i]]) ++z[i]; if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1; } return z; } ``` For this standard string match problem, we can use Z Algorithm to solve it in O(m + n) on the string P + (something won't be matched in both string) + S. If there is an indice i with Z[i] = n, then we find one occurence. Example: S = zabcabdabc P = abc m = 10 n = 3 Let K = P + (something won't be matched in both string) + S K = P + $ + S = abc$zabcabdabc Z would be {0, 0, 0, 0, 3, 0, 0, 2, 0, 0, 3, 0, 0} There are 2 indices ``i`` with Z[i] = n. Hence, there are 2 occurences of a pattern P in S. Here's the code implemented in C++. ``` void solve() { string p, s; cin >> p >> s; string k = p + "$" + s; vector z = z_function(k); int n = p.size(), m = k.size(), cnt = 0; REP(i, m) if(z[i] == n) cnt++; OUT(cnt); } ```

Hashing values using SHA-2 in PySpark

SHA stands for Secure Hashing Algorithm and 2 is just a version number. SHA-2 revises the construction and the big-length of the signature from SHA-1. You may also see SHA-224, SHA-256, SHA-384 or SHA-512. Those are referring the bit-lengths of SHA-2. It's a bit confusing. SHA-2 produces irreversible and unique hashes as it is a one-way hash function. The original data remains secure and unknown. However, given than a SHA-2 function with L message digest bits, you can have maximum 2^L possibilities, which means somebody can perform a brute force search even though it is not quite practical. Moreover, with a precomputed table, called rainbow table for caching the output of hash functions, simple input can be easily cracked. Therefore, to prevent precomputation attacks, we need salting. Salting is just an additional input concatenating to the original input. It should be long and random every time calling the hash function. ``` saltedhash(input) = hash_function(salt + input) ``` In PySpark, ``sha2`` was implemented since version 1.5. ``` def sha2(col, numBits): """Returns the hex string result of SHA-2 family of hash functions (SHA-224, SHA-256, SHA-384, and SHA-512). The numBits indicates the desired bit length of the result, which must have a value of 224, 256, 384, 512, or 0 (which is equivalent to 256). >>> digests = df.select(sha2(df.name, 256).alias('s')).collect() >>> digests[0] Row(s=u'3bc51062973c458d5a6f2d8d64a023246354ad7e064b1e4e009ec8a0699a3043') >>> digests[1] Row(s=u'cd9fb1e148ccd8442e5aa74904cc73bf6fb54d1d54d333bd596aa9bb4bb4e961') """ sc = SparkContext._active_spark_context jc = sc._jvm.functions.sha2(_to_java_column(col), numBits) return Column(jc) ``` First, we need to import the functions. ``` from pyspark.sql.functions import concat, col, lit, bin, sha2 ``` This is an example using ``withColumn`` with ``sha2`` function to hash the salt and the input with 256 message digest bits. ``` df = df.withColumn( col_name, sha2(concat(lit(generate_salt()), bin(col(col_name))), 256) ) ``` The hash value looks like ``8ba06918c277ee2e9b6eecb798fe64dc4a8c34d95b4514ecc267487aee9b84b9``.

Finding All Pairs Shortest Path Using Floyd–Warshall Algorithm

Floyd–Warshall Algorithm is an algorithm for finding shortest paths in a weighted graph with positive or negative edge weights (but with no negative cycles). Let's say we have 4 nodes and given the 2D array ``edges`` containing three values - {from, to, weight} representing a bidirectional and weighted edges between nodes ``from`` and ``to``. Supposing we have a distance threshold ``k`` and we would like to find out the smallest number of nodes that are reachable through some path whose the distance is at most ``k``.  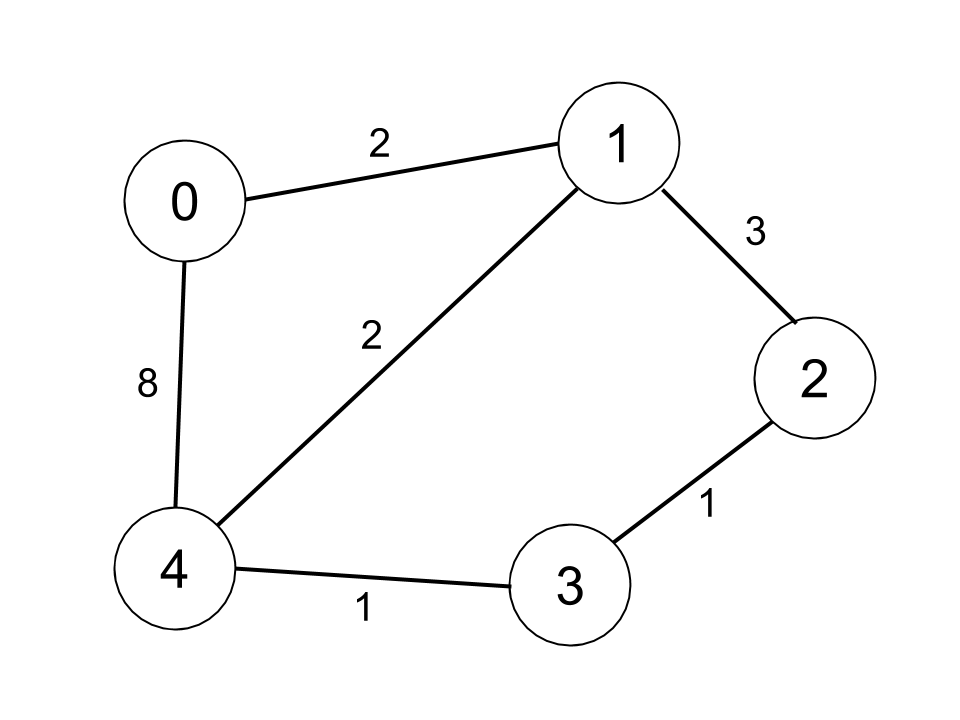The pseudocode for Floyd–Warshall algorithm is ``` let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity) for each edge (u, v) do dist[u][v] ← w(u, v) // The weight of the edge (u, v) for each vertex v do dist[v][v] ← 0 for k from 1 to |V| for i from 1 to |V| for j from 1 to |V| if dist[i][j] > dist[i][k] + dist[k][j] dist[i][j] ← dist[i][k] + dist[k][j] end if ``` To implement in C++, we first define ``dist``. As dist[i][j] stores the distance between two points, we can initialised the maximum value of ``k``. Let's say the constraint is ``1 <= k <= 10^4``. We can initialise any values which is greater than 10^4. ``` vector<vector<int>> dist(n, vector<int>(n, 10005)); ``` Then we need to reset the left diagonal to zero ``` for(int i = 0; i < n; i++) dist[i][i] = 0; ``` so that we can build the dist[i][j]. Let's say the edge is bidirectional. ``` for(auto e : edges) dist[e[0]][e[1]] = dist[e[1]][e[0]] = e[2]; ``` Calculate the distance for each pair with Time Complexity: O(n ^ 3) ``` for(int k = 0; k < n; k++) { for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]); } } } ``` If dist[i][j] is storing a boolean value, we can use ``` dist[i][j] = dist[i][j] || dist[i][k] && dist[k][j]; ``` Once we got dist[i][j], we can easily find out the answer. ``` int ans = 0, mi = n; for(int i = 0; i < n; i++) { int cnt = 0; for(int j = 0; j < n; j++) { cnt += dist[i][j] <= k; } if(cnt <= mi) { mi = cnt; ans = i; } } ``` Here are some practice problems. - [743. Network Delay Time](https://leetcode.com/problems/network-delay-time/) - [1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance](https://leetcode.com/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/) - [1462. Course Schedule IV](https://leetcode.com/problems/course-schedule-iv/)

Refactoring messy Test Suite in Python

Recently, I did some code reviews on my peer's code. We've created 100+ pySpark jobs and each job has its own test cases. When I looked at the file, it was super long. Let's take a look at main function. It is pretty general test suite main function. ``` if __name__ == "__main__": loader = unittest.TestLoader() suite = create_unit_suite() runner = unittest.TextTestRunner(verbosity=2) runner.run(suite) ``` However, when diving into create_unit_suite function, I was utterly dumbfounded. ``` def create_unit_suite(): suite = unittest.TestSuite() suite.addTests(loader.loadTestsFromModule(tests.test_job_1)) suite.addTests(loader.loadTestsFromModule(tests.test_job_2)) suite.addTests(loader.loadTestsFromModule(tests.test_job_3)) # ... suite.addTests(loader.loadTestsFromModule(tests.test_job_100)) suite.addTests(loader.loadTestsFromModule(tests.test_job_101)) suite.addTests(loader.loadTestsFromModule(tests.test_job_102)) # ... ``` And the import statements look like ``` import tests.test_job_1 import tests.test_job_2 import tests.test_job_3 # ... import tests.test_job_100 import tests.test_job_101 import tests.test_job_102 # ... ``` Every time a new job is created, the developers need to import it and and add a new addTests line. The folder structure is way more complicated and there is no guarantee that all developers remember to add the tests. You can't tell which jobs are missing test cases simply by looking at this file. Thanks to unittest, there is a function called ``discovery`` introduced in v3.2. It can be used like TestLoader.discover() or from the command line. From the documentation, it states that Unittest supports simple test discovery. In order to be compatible with test discovery, all of the test files must be modules or packages (including namespace packages) importable from the top-level directory of the project (this means that their filenames must be valid identifiers). In order to expose the test files, we need to make them modules. We can do that simply by adding __init__.py. Here's what's left. Specify the path and pattern for unittest to discover. No long import statements and addTests code. ``` import unittest from tests import * if __name__ == "__main__": testsuite = unittest.TestLoader().discover("tests", pattern="test_*.py") runner = unittest.TextTestRunner(verbosity=2).run(testsuite) ``` Simply run the below command to get the result. ``` python -m unittest ``` However, running all the test cases may take a great of time. In order to have more flexibility, it should be able to run in a specific module. We can use ``argparse`` to take ``--module`` flag to determine which module we are going to run test cases on. ``` import argparse ``` Put the logic in main() ``` def main(): parser = argparse.ArgumentParser() parser.add_argument("--module", action="store", default="all", help="the module of a collection of test cases to be executed") args = parser.parse_args() target_module = args.module target_path = "tests" if target_module == "all" else "tests/{}".format(target_module) testsuite = unittest.TestLoader().discover(target_path, pattern="test_*.py") runner = unittest.TextTestRunner(verbosity=2).run(testsuite) if __name__ == "__main__": main() ```

Unbounded Knapsack

Given an array of integers and a target sum, determine the sum nearest to but not exceeding the target that can be created. To create the sum, use any element of your array zero or more times. For example, if arr=[2,3,4] and your target sum is 10, you might select [2,2,2,2,2], [2,2,2,3] or [3,3,3,1] . In this case, you can arrive at exactly the target. Sample Input ``` 2 3 12 1 6 9 5 9 3 4 4 4 8 ``` Sample Output ``` 12 9 ``` Explanation In the first test case, one can pick {6, 6}. In the second, we can pick {3,3,3}. This is a unbounded knapsack so we cannot use the classic way to solve this problem. To solve it, we can break the problem into smaller problems first. If we put the first item into the knapsack, then the remaining capacity would be ``W-w1``. So we can break it down to find out the maximum value ``max1`` if we pack the same item ``N`` times in a knapsack of capacity ``W-w1``. For the second item, we do the same thing to get ``max2`` so that it has a remaining capacity of ``W-w2``, and so on. Each item has a own value now but we have to add the original value to it. ``` itemMax1 = max1 + v1 ``` The maximum value is ``` W = max(itemMax1,itemMax2,...,itemMaxN) ``` where ``W`` is the maximum value packed in the knapsack of capacity. Psuedo code ```cpp f(v[], w[], c) { // v: array of values // w: array of weights // c: capacity // n: length of the array // base case // if it is full, the total value of a 0 capacity knapsack is 0 if(c==0) return 0; int[] m; // break it down to smaller problem // ---------------------------------------- for(int i=0;i<n;i++){ // if we can put item 1 if(w[i]<c) m[i]=f(v,w,c-w[i]); // not enough space else m[i]=0; } // add back the original value // ---------------------------------------- for(int i=0;i<n;i++){ // if we can put item 1 if(w[i]<c) mm[i]=m[i] + v[i]; // not enough space else mm[i]=0; } // find the maximum value // ---------------------------------------- int ans=mm[0]; for(int i=1;i<n;i++){ if(mm[i]>ans) ans=mm[i]; } return ans; } ``` However, we can use bottom-up dynamic programming solution for this problem to improve the above solution. As we may see that we only have one parameter ``c`` for the recursive method where ``c`` ranges from ``W`` to ``0`` and ``v[]`` and ``w[]`` remain unchanged. Therefore, we can store the results computed by the recursive function in a 1d array. ```cpp int dp[W+1]; ``` We can set our base case to 0. ```cpp dp[0] = 0; ``` We can turn ```cpp f(v,w,c-w[i]); ``` to ```cpp dp[c-w[i]] ``` and also from ```cpp int ans=mm[0]; for(int i=1;i<n;i++){ if(mm[i]>ans) ans=mm[i]; } return ans; ``` to ```cpp dp[c]=mm[0]; for(int i=1;i<n;i++){ if(mm[i]>dp[c]) dp[c]=mm[i]; } ``` and the result would be ```cpp return dp[c]; ``` So we have the following structure ```cpp dp[0] = 0 for C=0 ... W: for i=0 .. N: if w[i]<=C: dp[i] = max ( dp[i], ( dp[C-w[i]] + v[i] ) ) else dp[i] = 0 ```

The Longest Increasing Subsequence Problem

The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence in a given array of integers such that all elements of the subsequence are sorted in strictly ascending order. For example, the length of the LIS for [15,27,14,38,26,55,46,65,85] is 6 since the longest increasing subsequence is [15,27,38,55,65,85] Sample Input ``` 5 2 7 4 3 8 ``` Sample Output ``` 3 ``` Explanation In the array [2,7,4,3,8], the longest increasing subsequence is [2,7,8]. It has a length of 3. Given that an array with a length of `n`, we can create two vectors with the same size - one called ``l`` for holding the length, another one ``s`` for holding the sub-sequence index. ``` arr [2,7,4,3,8] n [1,1,1,1,1] s [0,0,0,0,0] ``` If we list out the index, we should see ``` idx 0,1,2,3,4 arr [2,7,4,3,8] ``` let's say we have ``i`` and ``j`` where ``i`` starts from ``1..n-1`` and j starts from ``0..i``. ``` j,i idx 0,1,2,3,4 arr [2,7,4,3,8] ``` we check if ``arr[j]`` is lesser than ``arr[i]``. If so, check if ``l[j]+1`` is greater than ``l[i]`` In this case, ``arr[j]`` is 2 which is lesser than ``arr[i]`` which is 7. So we add ``l[j]`` by 1 to see if it is greater than ``l[i]``. It is. So we set ``l[j]+1`` to ``l[i]`` and set the index ``j`` to ``s[i]``. Repeat the above steps till ``i`` reaches ``n-1``. Find out the maximum value of ``l``. That is the length of the LIS. ```cpp int lis(vi a, int n){ vi l(n); vi s(n); int max=0; l[0]=1; FOR(i, 1, n){ l[i] = 1; REP(j,i){ if(a[j] < a[i]){ if(l[j]+1>l[i]){ l[i]=l[j]+1; s[i]=j; if(l[i]>max) max=l[i]; } } } } return max; } int main() { // SKIPPED } ``` However, this approach is ``O(N^2)`` which gives you Terminated due to timeout (TLE) Error. We need a faster approach to resolve this problem. Supposing there is a vector called ``vi``. The strategy is - If ``vi`` is empty, set the input ``a`` to ``vi[0]``. - If ``vi`` is not empty and the input ``a`` is the largest value of ``vi``, append ``a`` at the end - If ``vi`` is not empty and the input ``a`` is in between, find the correct index and replace the existing value. We can implement a binary search function to look for the correct index or we can just use STL. The answer is the size of ``vi``. Final Solution ```cpp int main() { FAST_INP; int n,a; cin >> n; vi v; REP(i,n){ vi::iterator it; cin >> a; if(i==0) v.push_back(a); else { it=lower_bound(v.begin(),v.end(),a); int k=it-v.begin(); if(k==v.size()) v.push_back(a); else v[k]=a; } } cout << v.size(); return 0; } ```

Breadth First Search (BFS)

Breadth First Search (BFS) can be used to explore nodes in different layers, compute shortest paths and connected components of undirected graph. The run time complexity is in linear time O(|V| + |E|) where |V| is the number of vertices and |E| is the number of edges in the graph. Initally all nodes are not visited, starting from vertex 1 in a graph G, mark 1 as visited. Let ``q`` be a FIFO queue, initialized with 1. While ``q`` is not empty, remove the first node of ``q`` called ``v``. For each edge ``u``, if ``u`` is not visited, mark it visited and add it to ``q.`` ```cpp memset(vis, 0, sizeof(vis)); queue<int> q; q.push(1); vis[1] = 1; while(!q.empty()) { int v = q.front(); q.pop(); for(auto u : g[v]) { if(!vis[u]) { vis[u] = 1; q.push(u); } } } ``` If vis[x] is 1, we can say that G has a path from 1 to x. Applications: - Shortest Paths ``` dist[v] = 0 if v = s, else INT_MAX for edge (v, u) if v is not visited set dist[u] = dist[v] + 1 ``` The shortets path result is stored in ``dist[u]``. - Connected Components via BFS ``` for i = 1 to n if not visited bfs(g, i) ```

Handling NULL values in GREATEST() function in Oracle Database

We can use GREATEST function to return the greatest value in a list of expressions. For example, below statement will return the value 3. ``` SELECT GREATEST(1, 2, 3) FROM DUAL; ``` However, if there is a NULL value in it, the return value will be NULL. As NULL is unknown, there is no way to do the comparison. If you call a SQL function with a null argument, then the SQL function automatically returns null. The workaround here is to use ``NVL`` to return an alternative value when an expression is NULL. Let's say we want to find out the max value between DATE 1 - 3. We can change the statement from ``` SELECT GREATEST( DATE1, DATE2, DATE3 ) FROM MY_TABLE; ``` to ``` SELECT GREATEST( NVL(DATE1, TO_DATE('1970-01-01', 'YYYY-MM-DD')), NVL(DATE2, TO_DATE('1970-01-01', 'YYYY-MM-DD')), NVL(DATE3, TO_DATE('1970-01-01', 'YYYY-MM-DD')) ) FROM MY_TABLE; ``` By adding ``NVL``, we can ensure that the expected return value is not NULL.