E-Olymp Competition - Dynamic programming (Linear) - Unofficial Editorial

Contest Link: [https://www.e-olymp.com/en/contests/19775](https://www.e-olymp.com/en/contests/19775) Full Solution: [https://github.com/wingkwong/competitive-programming/tree/master/e-olymp/contests/19775-dynamic-programming-linear](https://github.com/wingkwong/competitive-programming/tree/master/e-olymp/contests/19775-dynamic-programming-linear) # [A - Decreasing Number](https://www.e-olymp.com/en/contests/19775/problems/213338) ## Problem Statement There are three types of operations you can perform on an integer: 1. If it's divisible by 3, divide it by 3. 2. If it's divisible by 2, divide it by 2. 3. Subtract 1. Given a positive integer n, find the minimal number of operations needed to produce the number 1. ## Analysis Let $ \texttt{dp[n]} $ be the smallest number of operations to convert the number $ n $ to $ 1 $. For the base case, we know that for $ n = 1 $, there is no operation. Hence, we can define $ dp[1] = 0 $. For $ n = 2 $, there is only one way to do it which is the third operation. For $ n = 5 $, we can convert it like $ 5 \to 4 \to 2 \to 1 $, therefore we got $ dp[5] = 3 $. Therefore, the transition functions $ dp[i] $ for $ i = 2 \ldots n $ would be $$\begin{equation}\begin{aligned} dp[i] = dp[\frac{i}{3}] + 1 \\\\ dp[i] = dp[\frac{i}{2}] + 1 \\\\ dp[i] = dp[i - 1] + 1 \end{aligned}\end{equation}$$ We can only apply the first two operations only when the number can be divisible by $ 3 $ and $ 2 $ respectively. For every number greater than 1, we can subtract 1. Therefore, we can take the minimum one from previous results and add 1 to form $ dp[i] $. ## Implementation ```cpp int dp[1000005]; int go(int n) { dp[1] = 0; FORN(i, 2, n) { dp[i] = dp[i - 1] + 1; if(i % 2 == 0) dp[i] = min(dp[i], dp[i / 2] + 1); if(i % 3 == 0) dp[i] = min(dp[i], dp[i / 3] + 1); } return dp[n]; } void solve() { int x; while(cin >> x) { OUT(go(x)); } } ``` # [B - House Robber](https://www.e-olymp.com/en/contests/19775/problems/213339) ## Problem Statement You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses are broken into on the same night. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police. ## Analysis Let $ dp[i] $ be the maximum amount of money you can rob up to house $ i $ (0-base). We can think about the base cases first. We can set $ dp[0] = a[0] $ as we can only rob this house and $ dp[1] = max(a[0], a[1]) $ as we can only rob either one. Since we cannot rob adjacent houses, that means we can rob the current house $ i $ only if the house $ i - 1 $ hasn't been robbed. If we rob the current house, the total amount would be $ dp[i - 2] + a_i $. If not, that would be $ dp[i - 1] + 0 $. We just need to take the maximum one. ## Implementation Notice that the sum can be large so we cannot use int. ```cpp ll dp[1000005]; void solve() { int n; cin >> n; vl a(n); READ(a); dp[0] = a[0]; dp[1] = max(a[0], a[1]); FOR(i, 2, n) dp[i] = max(dp[i - 1], dp[i - 2] + a[i]); OUT(dp[n - 1]); } ``` # [C - Dice Combinations](https://www.e-olymp.com/en/contests/19775/problems/213340) ## Problem Statement Your task is to count the number of ways to construct sum $ n $ by throwing a dice one or more times. Each throw produces an outcome between $ 1 $ and $ 6 $. ## Analysis This question is like a knapsack problem. We can see that as we have infinite numbers of items with weights from $ 1 $ to $ 6 $ and we need to find out how many possible ways to make the knapsack completely full. Let $dp[i]$ be the number of ways to make it to sum $ i $ using numbers from $ 1 $ to $ 6 $. There is only one way to make the sum zero. Hence, we got $ dp[0] = 1 $. Let's say if last item was a $ 1 $, then we know there are $ dp[i - 1] $ ways to make the sum to $i$. If the last item was a $ 2 $, that would be $dp[i - 2]$ ways. The same logic applies for all the number from $ 1 $ to $ 6 $. Therefore we know that $$ dp[i] = \sum\limits_{j = 1}^{6} {dp[i - j]} $$ ## Implementation ``` int dp[1000005]; void solve() { int n; cin >> n; dp[0] = 1; FORN(i, 1, n) { FORN(j, 1, 6) { if(i - j >= 0) { (dp[i] += dp[i - j]) %= 1000000007; } } } OUT(dp[n]); } ``` # [D - Nails](https://www.e-olymp.com/en/contests/19775/problems/213341) ## Problem Statement Some nails are hammered on a straight plank. Any two nails can be joined by a thread. Connect some pairs of nails with a thread, so that to each nail will be tied with at least one thread, and the total length of all threads will be minimal. ## Analysis We can sort the coordinates of all the nails first. Let $ dp[i] $ be the minimum total length of all threads from the first nail to the i-th one. For the base cases we have $ dp[0] = 0 $, $ dp[1] = a[1] - a[0] $ and $ dp[2] = a[2] - a[1] $. Starting from $ i = 3 $, we can either connect the first $ i - 2 $ nails to have $ dp[i - 2] + a[i] - a[i - 1]$ or the first $ i - 1 $ nails to have $ dp[i - 1] + a[i] - a[i - 1] $. Therefore, we have to take the minimum length for each $ i $ where $3 \leqslant i \leqslant n $ holds to have $$ dp[i] = min(dp[i - 1], dp[i - 2]) + a[i] - a[i - 1] $$ ## Implementation ``` int dp[1000005]; void solve() { int n; cin >> n; vi a(n); READ(a); SORT(a); dp[1] = a[1] - a[0], dp[2] = a[2] - a[0]; FOR(i, 3, n) dp[i] = min(dp[i - 1], dp[i - 2]) + a[i] - a[i - 1]; OUT(dp[n - 1]); } ``` # [E - Journey from west to east](https://www.e-olymp.com/en/contests/19775/problems/213342) ## Problem Statement There are n cities standing on a straight line from west to east. The cities are numbered from 1 to n, in order from west to east. Each point on the line has its own one-dimensional coordinate, and the point closer to the east has a large coordinate. The coordinate of the i-th city is xi. You are now in city 1, and want to visit all cities. You have two ways to travel: Walk in a straight line. At the same time, your level of fatigue will increase by a units each time you move a distance of 1, regardless of the direction. Teleport to any point you want. Your fatigue level will increase by b units, regardless of teleported distance.  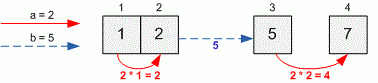## Analysis Let $ dp[i] $ be the lowest possible level of fatigue accumulated from the first city to the $i-th$ city. We can walk in a straight line to make our level of fatigue increase by $ a * (x[i] - x[i - 1]) $ or teleport to a point to make that increase by b. Therefore, the transition is a bit obvious. $$ dp[i] = dp[i - 1] + min(a * (x[i] - x[i - 1], b) $$ ## Implementation ``` ll dp[1000005]; void solve() { ll n, a, b; cin >> n >> a >> b; vl x(n); READ(x); dp[0] = dp[1] = 0; FORN(i, 2, n) { dp[i] = dp[i - 1] + min(a * (x[i - 1] - x[i - 2]), b); } OUT(dp[n]); } ``` # [F - Grasshopper](https://www.e-olymp.com/en/contests/19775/problems/213343) ## Problem Statement Grasshopper lives in the teacher's room. It likes to jump on one dimensional checkerboard. The length of the board is n cells. To its regret, it can jump only on 1, 2, ..., k cells forward. Once teachers wondered in how many ways a grasshopper can reach the last cell from the first one. Help them to answer this question. ## Analysis Let $ dp[i] $ be the number of ways for grasshopper to leap from the first cell to the $i-th$ cell. We know that there is only one way to move for $ i = 1 $ and $ i = 2 $. For $ 3 \leqslant i \leqslant k $, we can reach $i$-th cell from the previous cells. Therefore we can have $$ dp[i] = dp[1] + dp[2] + \ldots + dp[i - 1] = \sum\limits_{j = 1}^{i - 1} {dp[j]} $$ This would work if k is small enough. For large $ k $, we need a better way to calculate $ dp[i] $. Based on the observation, the first five values are $1, 1, 2, 4, 8$. Starting from $ i = 2 $, $ dp[i] $ is doubled from the previous value $ dp[i - 1] $. Formally, it can be obtained as follows. $ \begin{equation} dp[i] = dp[1] + dp[2] + \ldots + dp[i - 2] + dp[i - 1] \end{equation}\tag{1} $ $ \begin{equation} dp[i - 1] = dp[1] + dp[2] + \ldots + dp[i - 2] \end{equation}\tag{2} $ Put $ (2) $ into $ (1) $ $$ dp[i] = dp[i - 1] + dp[i - 1] $$ For $ 3 \leqslant i \leqslant k $, now we know that $ dp[i] = 2 * dp[i - 1] $. For $ i \gt k $, it can be reached from previous cells starting from $ i - k $. $$ dp[i] = dp[i - k] + \ldots + dp[i - 1] = \sum\limits_{j = i - k}^{i - 1} {dp[j]} $$ Similarly, we can rewrite it as follows. $ \begin{equation} dp[i] = dp[i - k] + \ldots + dp[i - 2] + dp[i - 1] \end{equation}\tag{3} $ $ \begin{equation} dp[i - 1] = dp[i - k - 1] + dp[i - k] + \ldots + dp[i - 2] \end{equation}\tag{4} $ Put $ (3) $ into $ (4) $ $$ dp[i] = (dp[i - k - 1] + dp[i - k] + \ldots + dp[i - 2]) + dp[i - 1] - dp[i - k - 1] $$ $$ dp[i] = dp[i - 1] + dp[i - 1] - dp[i - k - 1] $$ Therefore, we can conclude that we have $ dp[i] = 2 * dp[i - 1] $ for $ 3 \leqslant i \leqslant k $ and $ dp[i] = 2 * dp[i - 1] - dp[i - 1 - k] $ for $ i \gt k $. ## Implementation ``` int dp[1000005]; void solve() { int n, k; cin >> n >> k; dp[1] = dp[2] = 1; FORN(i, 3, n) { dp[i] = 2 * dp[i - 1]; if(i > k) dp[i] -= dp[i - 1 - k]; } OUT(dp[n]); } ``` # [G - Platforms](https://www.e-olymp.com/en/contests/19775/problems/213344) ## Problem Statement In older games one can run into the next situation. The hero jumps along the platforms that hang in the air. He must move himself from one side of the screen to the other. When the hero jumps from one platform to the neighboring, he spends |y_2 - y_1| energy, where y1 and y2 are the heights where these platforms hang. The hero can make a super jump that allows him to skip one platform, but it takes him 3 * |y3 - y1| energy. You are given the heights of the platforms in order from the left side to the right. Find the minimum amount of energy to get from the 1-st (start) platform to the n-th (last). Print the list (sequence) of the platforms that the hero must pass. ## Analysis Let $ dp[i] $ be the minimum amount of energy to get from the 1-st platform to the $i$-th. Starting from the base cases, we know that we need zero energy to reach the first platform, i.e. $ dp[1] = 0 $ and we need $ |y2 - y1| $ energy for $ dp[2] $. Starting from the third platform, we can either reach from the previous platform $ p[i - 1] $ or use super jump from $ p[i - 1] $. Hence, the minimum energy for $ dp[i] $ would be $$ dp[i] = min(dp[i - 1] + |y_{i} - y_{i-1}|, dp[i - 2] + 3 * |y_{i} - y_{i - 2}|) $$ So now we solve the first subtask. The remaining subtasks are to find out the number of platforms to pass and the list of these platforms. We can use another vector to store the index for each choice so that we can perform a path restoring at the end. The size of this vector is the answer to the second subtask and we need to reverse the vector to build the answer to the third subtask. ## Implementation ``` int dp[1000005]; void solve() { int n; cin >> n; vi a(n + 1); REPN(i, n) cin >> a[i]; dp[1] = 0; dp[2] = abs(a[2] - a[1]); vi p = {0, -1, 1}, ans; FORN(i, 3, n) { int x = dp[i - 1] + abs(a[i] - a[i - 1]); int y = dp[i - 2] + 3 * abs(a[i] - a[i - 2]); dp[i] = x < y ? x : y; p.pb(x < y ? i - 1 : i - 2); } OUT(dp[n]); int v = n; while(v != -1) { ans.pb(v); v = p[v]; } REVERSE(ans); OUT(SIZE(ans)); EACH(x, ans) OUTH(x); OUT(""); } ``` # [H - Frog](https://www.e-olymp.com/en/contests/19775/problems/213345) ## Problem Statement There are n stones, numbered 1, 2, ..., n. For each i (1 ≤ i ≤ n), the height of stone i is hi. There is a frog who is initially on stone 1. It will repeat the following action some number of times to reach stone n: if the frog is currently on stone i, jump to stone i + 1 or stone i + 2. Here, a cost of |hi − hj| is incurred, where j is the stone to land on. Find the minimum possible total cost incurred before the frog reaches stone n. ## Analysis Let $ dp[i] $ be the minimum possible total cost for frog to reach stone $ i $. We can reach the first stone without any cost and there is only one way to jump to the second stone. Hence, we know the base cases are $dp[1] = 0$ and $dp[2] = |h_2 - h_1|$. Starting from the thrid stone, we can either jump it from the last $i - 1$ stone or $i - 2$ stone. Therefore, we can add the current cost to previous results and take the minimum one. $$ dp[i] = min(dp[i - 1] + |h_i - h_{i - 1}|, dp[i - 2] + |h_i - h_{i - 2}|) $$ ## Implementation ``` int dp[1000005], h[1000005]; void solve() { int n; cin >> n; REPN(i, n) cin >> h[i]; dp[1] = 0; dp[2] = abs(h[2] - h[1]); FORN(i, 3, n) { dp[i] = min( dp[i - 1] + abs(h[i] - h[i - 1]), dp[i - 2] + abs(h[i] - h[i - 2]) ); } OUT(dp[n]); } ``` # [I - Platforms - 3](https://www.e-olymp.com/en/contests/19775/problems/213346) ## Problem Statement In older games one can run into the next situation. The hero jumps along the platforms that hang in the air. He must move himself from one side of the screen to the other. When the hero jumps from one platform to the neighboring, he spends |y2 - y1|^2 energy, where y1 and y2 are the heights where these platforms hang. The hero can make a super jump that allows him to skip one platform, but it takes him 3 * |y3 - y1|^2 energy. Symbol ^ here indicated exponentiation. You are given the heights of the platforms in order from the left side to the right. Find the minimum amount of energy to get from the 1-st (start) platform to the n-th (last). ## Analysis It is similar to the previous problem. Sometimes it is optimal to make a step back and jump to other platform. For exmaple, let's say there are four platforms and we can jump in the this order: $1 -> 3 -> 2 -> 4$. Let $ dp[i] $ be the minimum amount of energy to get from the 1-st platform to the $i$-th. We know that we don't need any energy to reach the first platform so we have $dp[1] = 0$. For the second platform, there are two cases to consider: 1. If there are only two platforms, the only way to reach the second platform is from the first platform. Hence, the required energy is $|a_2 - a_1| ^ 2$. 2. We can first jump to the third platform and jump back to the second platform. The required energy is $3 * |a_1 - a_3| ^ 2 + |a_2 - a_3| ^ 2$ Similarily, for $3 \leqslant i \leqslant n$, we can either 1. jump from the $(i - 1)$-th platform 2. super jump from the $(i - 2)$-th platform 3. jump from $(i - 1)$-th platform to $(i + 1)$-th platform and jump back to $i$-th platform if the jump is valid ($i < n$) The required energy for each case would be $$ dp[i - 1] + |a_i - a_{i - 1}| ^ 2 \\ $$ $$ dp[i - 2] + 3 * |a_i - a_{i - 2}| ^ 2 \\ $$ $$ dp[i - 1] + 3 * |a_{i + 1} - a_{i - 1}| ^ 2 + |a_i - a_{i + 1}| ^ 2 $$ and $ dp[i] $ takes the minimum one. ## Implementation ``` ll dp[1000005], a[1000005]; ll exp2(ll x) { return x * x; } void solve() { int n; cin >> n; REPN(i, n) cin >> a[i]; dp[1] = 0; dp[2] = exp2(abs(a[2] - a[1])); if(n == 2) { OUT(dp[n]); return; } dp[2] = min( exp2(abs(a[1] - a[2])), // 1 -> 2 3 * exp2(abs(a[1] - a[3])) + exp2(abs(a[3] - a[2])) // 1 -> 3 -> 2 ); FORN(i, 3, n) { dp[i] = min( dp[i - 1] + exp2(abs(a[i - 1] - a[i])), dp[i - 2] + 3 * exp2(abs(a[i - 2] - a[i])) ); if(i < n) { dp[i] = min( dp[i], dp[i - 1] + 3 * exp2(abs(a[i - 1] - a[i + 1])) + exp2(abs(a[i] - a[i + 1])) ); } } OUT(dp[n]); } ``` # [J - Buying tickets](https://www.e-olymp.com/en/contests/19775/problems/213347) ## Problem Statement There is a queue of n people to buy tickets to a musical premiere. Each person wants to buy exactly one ticket. Only one ticket-office was working, therefore ticketing was very slowly, bringing "guests" to despair. The most smart people quickly noticed that, as a rule, the cashier sells several tickets in one hand faster than when those same tickets are sold one by one. So they proposed for a number of people standing in a row to give money to the first one of them, so that he would buy tickets for all. However to deal with speculators, the cashier decided to sell maximum of three tickets per person, so to agree with each other in such way can only two or three successive persons. It is known that to sell one ticket for the i-th person in the queue takes ai seconds, to sell two tickets takes bi seconds, to sell three tickets takes ci seconds. Write a program that calculates the minimum time to serve all the customers. Please note that tickets for a group of united people always buys the first one. Also, no one buys extra tickets for speeding up the process (i.e. the tickets that are not wanted). ## Analysis Let $dp[i]$ be the minimum time in seconds to serve from the first to $i$-th customer. We only need $a_1$ seconds to server the first one if there is only one customer. If there are two customers, it takes either $a_1 + a_2$ seconds or $b_1$ seconds. Therefore, we know that the base cases are $$ dp[1] = a_1 $$ $$ dp[2] = min(a_1 + a_2, b_1) $$ If there are three or more customers, we have three cases to consider: 1. If the $i$-th customer buys one ticket, it takes $dp[i - 1] + a_i$ seconds 2. If the $(i-1)$-th customer buy two tickets, it takes $dp[i - 2] + b_{i - 1}$ seconds 3. If the $(i-2)$-th customer buy two tickets, it takes $dp[i - 3] + b_{i - 2}$ seconds We take the minimum value from these three cases. $$ dp[i] = min(dp[i - 1] + a_i, dp[i - 2] + b_{i - 1}, dp[i - 3] + b_{i - 2}) $$ ## Implementation ``` int dp[1000005], a[1000005], b[1000005], c[1000005], d[1000005]; void solve() { int n; cin >> n; REPN(i, n) cin >> a[i] >> b[i] >> c[i]; dp[0] = 0; dp[1] = a[1]; dp[2] = min(a[1] + a[2], b[1]); FORN(i, 3, n) dp[i] = min({ dp[i - 1] + a[i], dp[i - 2] + b[i - 1], dp[i - 3] + c[i - 2] }); OUT(dp[n]); } ```