Eulerian path / Hierholzer's Algorithm

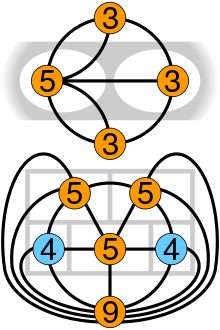
 ### Eulerian Trail / Path It is a trail in a finite graph that every edge will be visited exactly once. ### Eulerian Cycle / Circuit / Tour It is an Eulerian trail that starts and ends on the same vertex. ### Euler's Theorem A connected graph has an Euler cycle if and only if every vertex has even degree. ### Properties - An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component. - An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component. - An undirected graph has an Eulerian trail if and only if exactly zero or two vertices have odd degree, and all of its vertices with nonzero degree belong to a single connected component. - A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component. - A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph. ## Problem #1: LC2097 - Valid Arrangement of Pairs (Hard) You are given a 0-indexed 2D integer array pairs where $ pairs[i] = [start_i, end_i] $. An arrangement of pairs is valid if for every index i where 1 <= i < pairs.length, we have $end_i - 1 $ == $start_i$. Return any valid arrangement of pairs. Note: The inputs will be generated such that there exists a valid arrangement of pairs. ``` Input: pairs = [[5,1],[4,5],[11,9],[9,4]] Output: [[11,9],[9,4],[4,5],[5,1]] ``` ## Idea: Using Hierholzer's Alogorithm We can construct Eulerian trails and circuits using Fleury's algorithm or Hierholzer's algorithm. However, the latter one is more efficient than Fleury's algorithm. Here's the general idea. - Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph. - As long as there exists a vertex u that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u, and join the tour formed in this way to the previous tour. - Since we assume the original graph is connected, repeating the previous step will exhaust all edges of the graph. ## Solution: - Search the starting point of an Eulerian Path, i.e. $ out[i] == in[i] + 1 $. If we got $ out[i] == in[i] $ for all $ i $, then we can start at any arbitrary node (the first node is chosen in this solution). - Perform ``euler``, a post-order dfs function` on the graph. Walk through an edge and erase the visited edge. - Push the ``src`` and ``nxt`` to ``paths``. ``` void euler(unordered_map<int, vector<int>>& g, int src, vector<vector<int>>& paths) { while(!g[src].empty()) { int nxt = g[src].back(); g[src].pop_back(); euler(g, nxt, paths); paths.push_back({src, nxt}); } } vector<vector<int>> validArrangement(vector<vector<int>>& pairs) { vector<vector<int>> ans; int n = (int) pairs.size(); unordered_map<<int, vector<int>> g; unordered_map<int, int> in, out; for(auto x : pairs) { g[x[0]].push_back(x[1]); in[x[1]]++; out[x[0]]++; } int src = -1; for(auto x : g) { int i = x.first; if(out[i] - in[i] == 1) { src = i; break; } } if(src == -1) { src = g.begin()->first; } euler(g, src, ans); reverse(ans.begin(), ans.end()); return ans; } ``` ## Problem #2: LC332 - Reconstruct Itinerary (Hard) You are given a list of airline tickets where tickets[i] = [fromi, toi] represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it. All of the tickets belong to a man who departs from "JFK", thus, the itinerary must begin with "JFK". If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"]. You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.  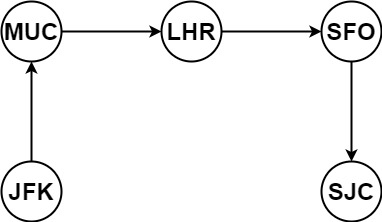``` Input: tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]] Output: ["JFK","MUC","LHR","SFO","SJC"] ``` ## Idea: Using Hierholzer's Alogorithm Similar to LC2097, in this problem, we don't need to search for the starting point as the itinerary must begin with ``JFK``. The black edges represent unvisited edge, green edges are visited edges, and brown edges are backtrack edges.  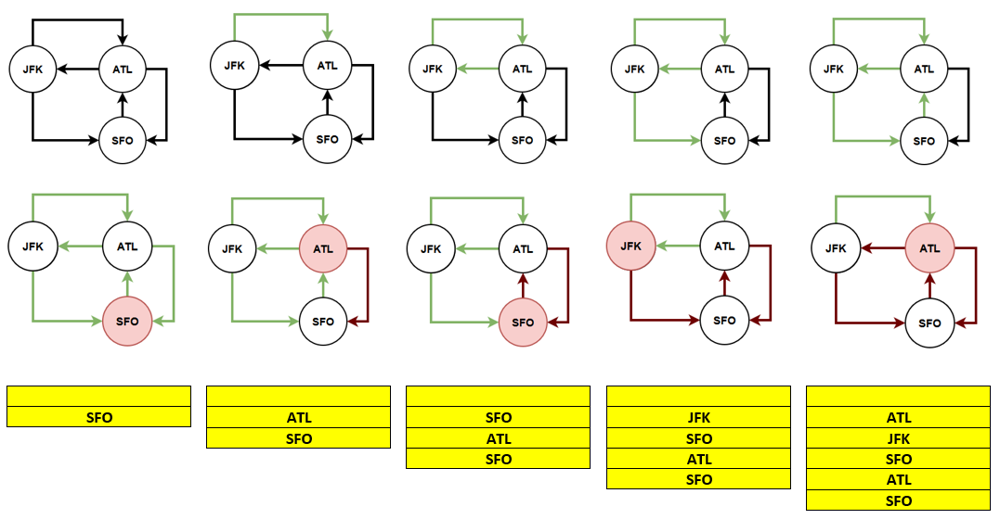## Solution: - Sort tickets based on the destination so that it could get the smaller edge first. - Perform ``euler``, a post-order dfs function` on the graph. Walk through an edge and erase the visited edge. - Push node to ``ans`` when all its edges are processed. ``` void euler(unordered_map<string, queue<string>>& g, string src, vector<string>& ans) { while(!g[src].empty()) { string nxt = g[src].front(); g[src].pop(); euler(g, nxt, ans); } ans.push_back(src); } vector<string> findItinerary(vector<vector<string>>& tickets) { vector<string> ans; sort(tickets.begin(), tickets.end(), [&](const vector& x, const vector& y) { return x[1] < y[1]; }); unordered_map<string, queue<string>> g; for(auto x : tickets) { g[x[0]].push(x[1]); } string src = "JFK"; euler(g, src, ans); reverse(ans.begin(), ans.end()); return ans; } ``` ## Problem #3: CSES1691 - Mail Delivery Your task is to deliver mail to the inhabitants of a city. For this reason, you want to find a route whose starting and ending point are the post office, and that goes through every street exactly once. Input The first input line has two integers n and m: the number of crossings and streets. The crossings are numbered 1,2,…,n, and the post office is located at crossing 1. After that, there are m lines describing the streets. Each line has two integers a and b: there is a street between crossings a and b. All streets are two-way streets. Every street is between two different crossings, and there is at most one street between two crossings. Output Print all the crossings on the route in the order you will visit them. You can print any valid solution. If there are no solutions, print "IMPOSSIBLE". ## Solution: ``` vector ans; vector> g; const int mxN = 1e6 + 5; void euler(int src) { while(g[src].size()) { int nxt = *g[src].begin(); g[nxt].erase(src); g[src].erase(nxt); euler(nxt); } ans.push_back(src); } void solve() { int n, m; cin >> n >> m; g.resize(mxN); for(int i = 0; i < m; i++) { int a, b; cin >> a >> b; --a, --b; g[a].insert(b); g[b].insert(a); } for(int i = 0; i < n; i++) { if(g[i].size() & 1) { cout << "IMPOSSIBLE" << endl; return; } } euler(0); if(ans.size() != m + 1) { cout << "IMPOSSIBLE" << endl; return; } reverse(ans.begin(), ans.end()); for(int i = 0; i < m + 1; i++) { cout << ans[i] + 1 << " \n"[i == m]; } } ```