Lagrange Interpolation

There are some well-known formulas $$ \sum_{i=1}^n i = 1 + 2 + \dots + n = \frac{n * (n + 1)}{2} $$ $$ \sum_{i=1}^n i^2 = 1^2 + 2^2 + \dots + n^2 = \frac{n * (n + 1) * (2n + 1)}{6} $$ $$ \sum_{i=1}^n i^3 = 1^3 + 2^3 + \dots + n^3 = (\frac{n * (n + 1)}{2}) ^ 2 $$ Then what is the value of the following sum of the k-th power? $$ \sum_{i=1}^n i^k = 1^k + 2^k + \dots + n^k \mod 10^9 + 7 $$ given $1 <= n <= 10^9$ and $0 <= k <= 10^6$ The target sum will be a degree $ (k + 1) $ polynomial and we can interpolate the answer with $ (k + 2) $ data points, i.e. $degree(f) + 1$ points. In order to find the data points, we need to calculate $f(0) = 0$, $f(x) = f(x - 1) + x ^ k$. If there is less than $k + 2$ data points, we can calculate the answer directly. ``` if (x <= k + 1) { int s = 0; for (int i = 1; i <= x; i++) { s = (s + qpow(i, k)) % mod; } return s; } ``` Otherwise, let's say $f(x_1) = y_1, f(x_2) = y_2, ..., f(x_n) = y_n$ and $f$ is the unique $(n - 1)$ degree polynomial and we are interested in $f(x) = \sum_{i=1}^n f_i(x)$ where $f_i(x) = y_i * \prod_{j=1, j!=i}^n \frac{x - x_j}{x_i - x_j} $. Therefore, we have our Lagrange interpolation as $ f(x) = \sum_{i=1}^n y^i \prod_{j=1, j!=i}^n \frac{x - x_j}{x_i - x_j} $. However, we need $O(n^2)$ to calculate $f(x)$. Let's substitute $x_i = i$ and $y_i = f(i)$ and we got $ f(x) = \sum_{i=1}^n f(i) \frac{\prod_{j=1, j!=i}^n x - j}{\prod_{j=1, j!=i}^n i - j} $. What can we do for numerator and denonminator here? For numerator, we can per-calculate the prefix and suffix product of $x$, for each $i$, we can calculate the nubmerator in $O(1)$. $$ \prod_{j=1, j!=i}^n x - x_j = [(x - 1)(x - 2)...(x-(i-1))] * [(x - (i + 1))*(x - (i + 2))...(x - n)] $$ ``` vector pre(k + 2), suf(k + 2); pre[0] = x; suf[k + 1] = x - (k + 1); for (int i = 1; i <= k; i++) pre[i] = pre[i - 1] * (x - i) % mod; for (int i = k; i >= 1; i--) suf[i] = suf[i + 1] * (x - i) % mod; ``` For denominator, we can precompute the factorials using their inverse in $O(1)$ also. $$ \prod_{j=1, j!=i}^n i - j = [(i - 1)(i - 2)(i - 3)...(i - (i - 1))] * [i - (i + 1)(i - (i + 2)...(i - n)] = (-1)^{n - i} (n - i)!(i - 1)! $$ ``` int qpow(int base, int exp) { int res = 1; while (exp) { if (exp & 1) res = (res * base) % mod; base = (base * base) % mod; exp >>= 1; } return res; } unordered_map<int, int> rv_m; int rv(int x) { if (rv_m.count(x)) { return rv_m[x]; } return rv_m[x] = qpow(x, mod - 2); } vector inv(k + 2); inv[0] = 1; for (int i = 1; i <= k + 1; i++) inv[i] = inv[i - 1] * rv(i) % mod; ``` Overall, we can calculate $f(x)$ in $O(n)$. Complete Code: ``` #include <bits/stdc++.h> using namespace std; #define int long long const int mod = 1e9 + 7; int qpow(int base, int exp) { int res = 1; while (exp) { if (exp & 1) res = (res * base) % mod; base = (base * base) % mod; exp >>= 1; } return res; } unordered_map<int, int> rv_m; int rv(int x) { if (rv_m.count(x)) { return rv_m[x]; } return rv_m[x] = qpow(x, mod - 2); } int lagrange_interpolate(int x, int k, bool bf = false) { if (k == 0) return x; // find 1 ^ k + 2 ^ k + ... + x ^ k // (k + 1) degree polynomial -> (k + 2) points if (x <= k + 1 || bf) { int s = 0; for (int i = 1; i <= x; i++) { s = (s + qpow(i, k)) % mod; } return s; } vector<int> pre(k + 2), suf(k + 2), inv(k + 2); inv[0] = 1, pre[0] = x; suf[k + 1] = x - (k + 1); for (int i = 1; i <= k; i++) pre[i] = pre[i - 1] * (x - i) % mod; for (int i = k; i >= 1; i--) suf[i] = suf[i + 1] * (x - i) % mod; for (int i = 1; i <= k + 1; i++) inv[i] = inv[i - 1] * rv(i) % mod; int ans = 0; int yi = 0; // 0 ^ k + ~ i ^ k int num, denom; for (int i = 0; i <= k + 1; i++) { yi = (yi + qpow(i, k)) % mod; // interpolate point: (i, yi) if (i == 0) num = suf[1]; else if (i == k + 1) num = pre[k]; else num = pre[i - 1] * suf[i + 1] % mod; // numerator denom = inv[i] * inv[k + 1 - i] % mod; // denominator if ((i + k) & 1) ans += (yi * num % mod) * denom % mod; else ans -= (yi * num % mod) * denom % mod; ans = (ans % mod + mod) % mod; } return ans; } void solve() { int n, k; cin >> n >> k; cout << lagrange_interpolate(n, k) << endl; } int32_t main() { ios_base::sync_with_stdio(false), cin.tie(nullptr); // int T; cin >> T; // while(T--) solve(); solve(); return 0; } ```

LeetCode - Weekly Contest 273 Editorial

## [Q1: A Number After a Double Reversal](https://leetcode.com/problems/a-number-after-a-double-reversal/) If you just do what it says, here's the code. ```cpp class Solution { public: bool isSameAfterReversals(int num) { if (num == 0) return 1; string s = to_string(num); int n = s.size(), j = 0; while (s[n - 1 - j] == '0') j++; string t = s.substr(0, n - j); return s == t; } }; ``` However, a better way to solve this is to check if there is any trailing zero. No matter how many zeros at the end, after removing them all, it won't be same if you reverse it. The only exceptional case is $num = 0$. ``` class Solution { public: bool isSameAfterReversals(int num) { return num == 0 || num % 10; } }; ``` ## [Q2: Execution of All Suffix Instructions Staying in a Grid](https://leetcode.com/problems/execution-of-all-suffix-instructions-staying-in-a-grid/) We can just simulate the whole process. For each $i-th$ instruction, we have max $ s.size() - i $ steps assuming $ i $ starts from $ 0 $. We keep updating the position $(x, y)$ and check if it is out of bound. If not, keep inceasing $cnt$ by 1. If there is no further move we can make, we can break the loop and push the result $cnt$ to $ans$. ``` class Solution { public: vector executeInstructions(int n, vector& startPos, string s) { int m = s.size(); vector ans; for (int i = 0; i < m; i++) { int x = startPos[0]; int y = startPos[1]; int cnt = 0; for (int j = i; j < m; j++) { if (s[j] == 'L') y--; if (s[j] == 'R') y++; if (s[j] == 'U') x--; if (s[j] == 'D') x++; if (0 <= x && x < n && 0 <= y && y < n) cnt++; else break; } ans.push_back(cnt); } return ans; } }; ``` However, the above brute-force solution gives $O(m^2)$ complexity. It works because $m$ is just limited to $1000$. There's a $O(m)$ solution. ``` class Solution { public: vector executeInstructions(int n, vector& startPos, string s) { int m = s.size(), h = m + n, v = m + n; vector hor((m + n) * 2, m), ver((m + n) * 2, m), ans(m); for (int i = m - 1; i >= 0; i--) { hor[h] = ver[v] = i; if (s[i] == 'L') h++; if (s[i] == 'R') h--; if (s[i] == 'U') v++; if (s[i] == 'D') v--; ans[i] = min({ m, hor[h - startPos[1] - 1], hor[h - startPos[1] + n], ver[v - startPos[0] - 1], ver[v + startPos[0] * -1 + n] }) - i; } return ans; } }; ``` ## [Intervals Between Identical Elements](intervals-between-identical-elements) First we need to know the indices for each number. We can easily construct it using ``unordered_map<int, vector<int>>``. Then it comes to the math part. Our goal is to calculate the absolute difference for numbers smaller than and greater than or equal to $k$ in linear time. Let's say the list is [1, 3, 5, 7, 9] and let $k$ be $7$. The absolute difference for numbers smaller than or equal to $7$ is $(7 - 1) + (7 - 3) + (7 - 5) - (7 - 7)$. We can arrange it to $ 7 * 4 - (1 - 3 - 5 - 7)$ which is same as $k * (i + 1) - pre[i + 1]$. Similarly, let $k$ be $3$ and we want to find out the absolute difference for numbers greater than or equal to $3$. $(3 - 3) + (3 - 5) + (3 - 7) + (3 - 9)$. We can arrange it to $3 * 4 - (3 + 5 + 7 + 9)$, which is same as $(pre[n] - pre[i]) - k * (n - i)$. Therefore, $ans[k]$ would be the sum of the left part and the right part. Prefix sum can be calculated as ``` for (int i = 0; i < n; i++) { pre[i + 1] = pre[i] + v[i]; } ``` ``` class Solution { public: vector<long long> getDistances(vector& arr) { unordered_map<int, vector<int>> m; vector<long long> ans(arr.size()); int n = arr.size(); for (int i = 0; i < n; i++) { m[arr[i]].push_back(i); } for (auto x : m) { vector v = x.second; int n = v.size(); vector<long long> pre(n + 1); for (int i = 0; i < n; i++) { pre[i + 1] = pre[i] + v[i]; } for (int i = 0; i < n; i++) { long long k = v[i]; ans[k] = (k * (i + 1) - pre[i + 1]) + (pre[n] - pre[i] - k * (n - i)); } } return ans; } }; ``` ## [Recover the Original Array](https://leetcode.com/problems/recover-the-original-array/) In short, we just need to try all possible $k$. If we sort $nums$, the smallest elelment must be in the lower array. It is easy to see $k$ can be $(nums[i] - nums[0]) / 2$. We try each $k$ to see if we can match all the pairs. If the size of lower array is same as that of higher array, then the ans would be $ans[j] = (l[j] + r[j]) / 2$. ``` class Solution { public: vector recoverArray(vector& nums) { int n = nums.size(); sort(nums.begin(), nums.end()); for (int i = 0; i < nums.size(); i++) { unordered_map<int, int> m; int d = nums[i] - nums.front(); if (d == 0 || d & 1) { continue; } vector l, r; for (int j = 0; j < n; j++) { if (m.count(nums[j] - d)) { r.push_back(nums[j]); if (--m[nums[j] - d] == 0) { m.erase(nums[j] - d); } } else { l.push_back(nums[j]); m[nums[j]]++; } } if (l.size() == r.size()) { vector ans; for (int j = 0; j < n / 2; j++) { ans.push_back((l[j] + r[j]) / 2); } return ans; } } return {}; } }; ```

The Easiest LeetCode Contest in 2021

This LeetCode contest is sponsored by Amazon Pay. Check out [Weekly Contest 272](https://leetcode.com/contest/weekly-contest-272) for the questions. ## Q1 - 2108. Find First Palindromic String in the Array Given an array of strings words, return the first palindromic string in the array. If there is no such string, return an empty string "". A string is palindromic if it reads the same forward and backward. ### Example 1: Input: words = ["abc","car","ada","racecar","cool"] Output: "ada" Explanation: The first string that is palindromic is "ada". Note that "racecar" is also palindromic, but it is not the first. ### Example 2: Input: words = ["notapalindrome","racecar"] Output: "racecar" Explanation: The first and only string that is palindromic is "racecar". ### Example 3: Input: words = ["def","ghi"] Output: "" Explanation: There are no palindromic strings, so the empty string is returned. ## Solution There are several ways to check if $s$ is a palindrome. ### Long and Efficient ```cpp bool isPalindrome(const string& s) { for (int i = 0; i < s.size() / 2; i++) { if (s[i] != s[s.size() - i - 1]) return false; } return true; } ``` ### Shorter but not efficient ```cpp bool isPalindrome(const string& s) { string t = s; reverse(t.begin(), t.end()); return s == t; } ``` ### Shortest but not efficient ```cpp bool isPalindrome(const string& s) { return s == string(s.rbegin(), s.rend()); } ``` ### Shortest but efficient ```cpp bool isPalindrome(const string &s) { return equal(s.begin(), s.begin() + s.size() / 2, s.rbegin()); } ``` We just need to iterate each string and check if the target $s$ is a palindrome, return the string if so. ``` class Solution { public: bool isPalindrome(const string& s) { return equal(s.begin(), s.begin() + s.size() / 2, s.rbegin()); } string firstPalindrome(vector& words) { for (auto s : words) { if (isPalindrome(s)) { return s; } } return ""; } }; ``` ## Q2 - 2109. Adding Spaces to a String You are given a 0-indexed string s and a 0-indexed integer array spaces that describes the indices in the original string where spaces will be added. Each space should be inserted before the character at the given index. For example, given s = "EnjoyYourCoffee" and spaces = [5, 9], we place spaces before 'Y' and 'C', which are at indices 5 and 9 respectively. Thus, we obtain "Enjoy Your Coffee". Return the modified string after the spaces have been added. ### Example 1: Input: s = "LeetcodeHelpsMeLearn", spaces = [8,13,15] Output: "Leetcode Helps Me Learn" Explanation: The indices 8, 13, and 15 correspond to the underlined characters in "LeetcodeHelpsMeLearn". We then place spaces before those characters. ### Example 2: Input: s = "icodeinpython", spaces = [1,5,7,9] Output: "i code in py thon" Explanation: The indices 1, 5, 7, and 9 correspond to the underlined characters in "icodeinpython". We then place spaces before those characters. ### Example 3: Input: s = "spacing", spaces = [0,1,2,3,4,5,6] Output: " s p a c i n g" Explanation: We are also able to place spaces before the first character of the string. ## Solution Two-pointer. i-th pointer is for string $s$ and j-th pointer is for spaces vector. Iterate string $s$, if $i$ matches $spaces[j]$, then add a space and increase $j$ by 1. ``` class Solution { public: string addSpaces(string s, vector& spaces) { string ans; int j = 0, m = spaces.size(); for (int i = 0; i < s.size(); i++) { if (j < m && i == spaces[j]) ans += " ", j++; ans += s[i]; } return ans; } }; ``` ## Q3 - 2110. Number of Smooth Descent Periods of a Stock You are given an integer array prices representing the daily price history of a stock, where prices[i] is the stock price on the ith day. A smooth descent period of a stock consists of one or more contiguous days such that the price on each day is lower than the price on the preceding day by exactly 1. The first day of the period is exempted from this rule. Return the number of smooth descent periods. ### Example 1: Input: prices = [3,2,1,4] Output: 7 Explanation: There are 7 smooth descent periods: [3], [2], [1], [4], [3,2], [2,1], and [3,2,1] Note that a period with one day is a smooth descent period by the definition. ### Example 2: Input: prices = [8,6,7,7] Output: 4 Explanation: There are 4 smooth descent periods: [8], [6], [7], and [7] Note that [8,6] is not a smooth descent period as 8 - 6 ≠ 1. ### Example 3: Input: prices = [1] Output: 1 Explanation: There is 1 smooth descent period: [1] ## Solution The first observation is each number is a smooth descent period. The final answer is at least $ n $ which is the size of the given vector. Therefore, the initial value for $dp[i]$ is $1$. The second observation is that we can add $dp[i - 1]$ to $dp[i]$ if $prices[i - 1] - prices[i] = 1$ starting from $i = 1$. ``` class Solution { public: long long getDescentPeriods(vector& prices) { int n = prices.size(); long long ans = 0; vector dp(n, 1); for (int i = 0; i < n; i++) { if (i > 0 && prices[i - 1] - prices[i] == 1) { dp[i] += dp[i - 1]; } ans += dp[i]; } return ans; } }; ``` ## Q4 - 2111. Minimum Operations to Make the Array K-Increasing You are given a 0-indexed array arr consisting of n positive integers, and a positive integer k. The array arr is called K-increasing if arr[i-k] <= arr[i] holds for every index i, where k <= i <= n-1. For example, arr = [4, 1, 5, 2, 6, 2] is K-increasing for k = 2 because: arr[0] <= arr[2] (4 <= 5) arr[1] <= arr[3] (1 <= 2) arr[2] <= arr[4] (5 <= 6) arr[3] <= arr[5] (2 <= 2) However, the same arr is not K-increasing for k = 1 (because arr[0] > arr[1]) or k = 3 (because arr[0] > arr[3]). In one operation, you can choose an index i and change arr[i] into any positive integer. Return the minimum number of operations required to make the array K-increasing for the given k. ### Example 1: Input: arr = [5,4,3,2,1], k = 1 Output: 4 Explanation: For k = 1, the resultant array has to be non-decreasing. Some of the K-increasing arrays that can be formed are [5,6,7,8,9], [1,1,1,1,1], [2,2,3,4,4]. All of them require 4 operations. It is suboptimal to change the array to, for example, [6,7,8,9,10] because it would take 5 operations. It can be shown that we cannot make the array K-increasing in less than 4 operations. ### Example 2: Input: arr = [4,1,5,2,6,2], k = 2 Output: 0 Explanation: This is the same example as the one in the problem description. Here, for every index i where 2 <= i <= 5, arr[i-2] <= arr[i]. Since the given array is already K-increasing, we do not need to perform any operations. ### Example 3: Input: arr = [4,1,5,2,6,2], k = 3 Output: 2 Explanation: Indices 3 and 5 are the only ones not satisfying arr[i-3] <= arr[i] for 3 <= i <= 5. One of the ways we can make the array K-increasing is by changing arr[3] to 4 and arr[5] to 5. The array will now be [4,1,5,4,6,5]. Note that there can be other ways to make the array K-increasing, but none of them require less than 2 operations. ## Solution We can break input vector into $k$ groups $a_i, a_{i + k}, a_{i + 2 * k}, ...$ for each $ i < k$. Calculate the LIS (Longest Increasing Subsequence) on each group and compare the length with the target size. We need to perform $a.size() - lengthOfLIS(a)$ operations to make it K-increasing. ``` class Solution { public: int lengthOfLIS(vector& nums) { int n = (int) nums.size(); vector lis; for(int i = 0; i < n; i++) { auto it = upper_bound(lis.begin(), lis.end(), nums[i]); if(it == lis.end()) lis.push_back(nums[i]); else *it = nums[i]; } return (int) lis.size(); } int kIncreasing(vector& arr, int k) { int ans = 0, n = arr.size(); for (int i = 0; i < k; i++) { vector a; for (int j = i; j < n; j += k) { a.push_back(arr[j]); } ans += a.size() - lengthOfLIS(a); } return ans; } }; ```

Eulerian path / Hierholzer's Algorithm

 ### Eulerian Trail / Path It is a trail in a finite graph that every edge will be visited exactly once. ### Eulerian Cycle / Circuit / Tour It is an Eulerian trail that starts and ends on the same vertex. ### Euler's Theorem A connected graph has an Euler cycle if and only if every vertex has even degree. ### Properties - An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component. - An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component. - An undirected graph has an Eulerian trail if and only if exactly zero or two vertices have odd degree, and all of its vertices with nonzero degree belong to a single connected component. - A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component. - A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph. ## Problem #1: LC2097 - Valid Arrangement of Pairs (Hard) You are given a 0-indexed 2D integer array pairs where $ pairs[i] = [start_i, end_i] $. An arrangement of pairs is valid if for every index i where 1 <= i < pairs.length, we have $end_i - 1 $ == $start_i$. Return any valid arrangement of pairs. Note: The inputs will be generated such that there exists a valid arrangement of pairs. ``` Input: pairs = [[5,1],[4,5],[11,9],[9,4]] Output: [[11,9],[9,4],[4,5],[5,1]] ``` ## Idea: Using Hierholzer's Alogorithm We can construct Eulerian trails and circuits using Fleury's algorithm or Hierholzer's algorithm. However, the latter one is more efficient than Fleury's algorithm. Here's the general idea. - Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph. - As long as there exists a vertex u that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u, and join the tour formed in this way to the previous tour. - Since we assume the original graph is connected, repeating the previous step will exhaust all edges of the graph. ## Solution: - Search the starting point of an Eulerian Path, i.e. $ out[i] == in[i] + 1 $. If we got $ out[i] == in[i] $ for all $ i $, then we can start at any arbitrary node (the first node is chosen in this solution). - Perform ``euler``, a post-order dfs function` on the graph. Walk through an edge and erase the visited edge. - Push the ``src`` and ``nxt`` to ``paths``. ``` void euler(unordered_map<int, vector<int>>& g, int src, vector<vector<int>>& paths) { while(!g[src].empty()) { int nxt = g[src].back(); g[src].pop_back(); euler(g, nxt, paths); paths.push_back({src, nxt}); } } vector<vector<int>> validArrangement(vector<vector<int>>& pairs) { vector<vector<int>> ans; int n = (int) pairs.size(); unordered_map<<int, vector<int>> g; unordered_map<int, int> in, out; for(auto x : pairs) { g[x[0]].push_back(x[1]); in[x[1]]++; out[x[0]]++; } int src = -1; for(auto x : g) { int i = x.first; if(out[i] - in[i] == 1) { src = i; break; } } if(src == -1) { src = g.begin()->first; } euler(g, src, ans); reverse(ans.begin(), ans.end()); return ans; } ``` ## Problem #2: LC332 - Reconstruct Itinerary (Hard) You are given a list of airline tickets where tickets[i] = [fromi, toi] represent the departure and the arrival airports of one flight. Reconstruct the itinerary in order and return it. All of the tickets belong to a man who departs from "JFK", thus, the itinerary must begin with "JFK". If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"]. You may assume all tickets form at least one valid itinerary. You must use all the tickets once and only once.  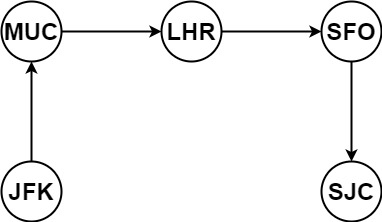``` Input: tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]] Output: ["JFK","MUC","LHR","SFO","SJC"] ``` ## Idea: Using Hierholzer's Alogorithm Similar to LC2097, in this problem, we don't need to search for the starting point as the itinerary must begin with ``JFK``. The black edges represent unvisited edge, green edges are visited edges, and brown edges are backtrack edges.  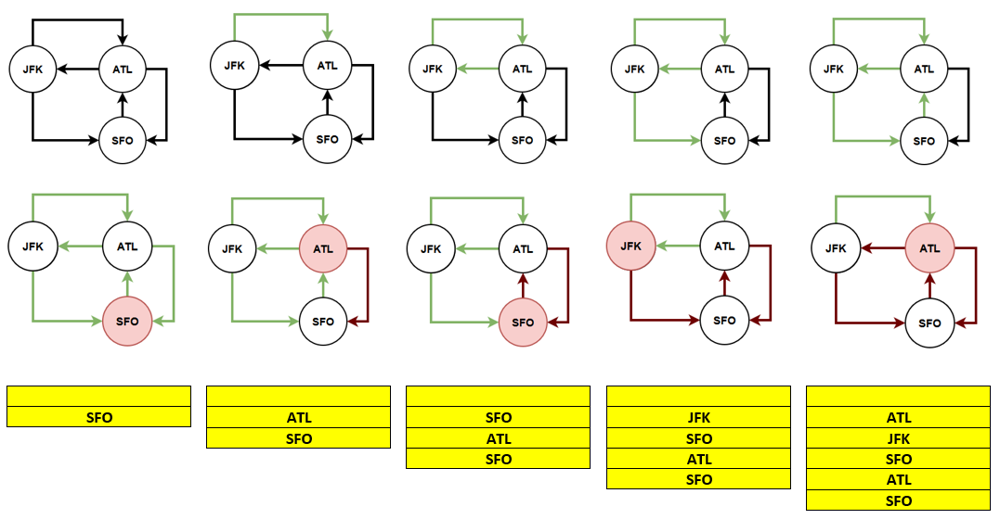## Solution: - Sort tickets based on the destination so that it could get the smaller edge first. - Perform ``euler``, a post-order dfs function` on the graph. Walk through an edge and erase the visited edge. - Push node to ``ans`` when all its edges are processed. ``` void euler(unordered_map<string, queue<string>>& g, string src, vector<string>& ans) { while(!g[src].empty()) { string nxt = g[src].front(); g[src].pop(); euler(g, nxt, ans); } ans.push_back(src); } vector<string> findItinerary(vector<vector<string>>& tickets) { vector<string> ans; sort(tickets.begin(), tickets.end(), [&](const vector& x, const vector& y) { return x[1] < y[1]; }); unordered_map<string, queue<string>> g; for(auto x : tickets) { g[x[0]].push(x[1]); } string src = "JFK"; euler(g, src, ans); reverse(ans.begin(), ans.end()); return ans; } ``` ## Problem #3: CSES1691 - Mail Delivery Your task is to deliver mail to the inhabitants of a city. For this reason, you want to find a route whose starting and ending point are the post office, and that goes through every street exactly once. Input The first input line has two integers n and m: the number of crossings and streets. The crossings are numbered 1,2,…,n, and the post office is located at crossing 1. After that, there are m lines describing the streets. Each line has two integers a and b: there is a street between crossings a and b. All streets are two-way streets. Every street is between two different crossings, and there is at most one street between two crossings. Output Print all the crossings on the route in the order you will visit them. You can print any valid solution. If there are no solutions, print "IMPOSSIBLE". ## Solution: ``` vector ans; vector> g; const int mxN = 1e6 + 5; void euler(int src) { while(g[src].size()) { int nxt = *g[src].begin(); g[nxt].erase(src); g[src].erase(nxt); euler(nxt); } ans.push_back(src); } void solve() { int n, m; cin >> n >> m; g.resize(mxN); for(int i = 0; i < m; i++) { int a, b; cin >> a >> b; --a, --b; g[a].insert(b); g[b].insert(a); } for(int i = 0; i < n; i++) { if(g[i].size() & 1) { cout << "IMPOSSIBLE" << endl; return; } } euler(0); if(ans.size() != m + 1) { cout << "IMPOSSIBLE" << endl; return; } reverse(ans.begin(), ans.end()); for(int i = 0; i < m + 1; i++) { cout << ans[i] + 1 << " \n"[i == m]; } } ```