Codeforces - 999E. Reachability from the Capital

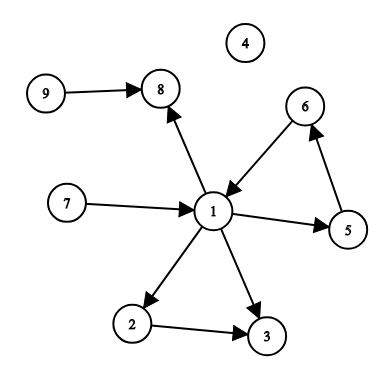
Problem Link: [https://codeforces.com/contest/999/problem/E](https://codeforces.com/contest/999/problem/E) ## Problem There are n cities and m roads in Berland. Each road connects a pair of cities. The roads in Berland are one-way. What is the minimum number of new roads that need to be built to make all the cities reachable from the capital? New roads will also be one-way.  ## Input The first line of input consists of three integers n, m and s (1≤n≤5000,0≤m≤5000,1≤s≤n) — the number of cities, the number of roads and the index of the capital. Cities are indexed from 1 to n. The following m lines contain roads: road 𝑖 is given as a pair of cities u𝑖, v𝑖 (1≤u𝑖,v𝑖≤n, u𝑖≠v𝑖). For each pair of cities (u,v), there can be at most one road from u to v. Roads in opposite directions between a pair of cities are allowed (i.e. from u to v and from v to u). ## Output Print one integer — the minimum number of extra roads needed to make all the cities reachable from city s. If all the cities are already reachable from s, print 0. ## Example Input ``` 9 9 1 1 2 1 3 2 3 1 5 5 6 6 1 1 8 9 8 7 1 ``` Output ``` 3 ``` ## Solution 1 Firstly, let's store the possible paths for each city u[i]. ``` int N, M, S; cin >> N >> M >> S; --S; while(M--) { int U, V; cin >> U >> V; --U, --V; g[U].push_back(V); } ``` Secondly, we can perform a DFS function to mark all the reachable nodes from the given source. ``` void dfs(int from) { reachable[from] = 1; for(auto to : g[from]) { if(!reachable[to]) { dfs(to); } } } ``` Then, for each unreachable node, run a DFS function on it to count how far it can go. Here we only count those nodes that are not reachable and not visited. ``` vector> v; for(int i = 0; i < n; i++){ if(!reachable[i]) { cnt = 0; memset(vis, 0, sizeof(vis)); dfs2(i); v.push_back({cnt, i}); } } ``` After that we can sort the vector by ``cnt`` in non-increasing order. ``` sort(v.begin(), v.end()); reverse(v.begin(), v.end()); ``` We can greedily mark the unreachable nodes based on this order. If the node A has more to unreachable nodes to reach, then we just need to add one vertex to it to make them all connected, which is the minimum number of paths to be added. ``` int ans = 0; for(auto x : v) { if(!reachable[x.second]) { ans++; dfs(x.second); } } ``` ## Solution 2 We can also find all the Strongly Connected Components (SCC) and add a path to those with 0 in-degree. It will be able to reach the maximum number of nodes. First, let's read the input and prepare G. ``` while(M--) { int U, V; cin >> U >> V; --U, --V; G[U].push_back(V); } ``` Then we can use Tarjan's algorithm to find all the SCCs. ``` struct SCC : vector { vector> comps; vector S; SCC() {} SCC(vector>& G) : vector((int)G.size(), -1), S((int)G.size()) { for(int i = 0; i < (int)G.size(); i++) if(!S[i]) dfs(G, i); } int dfs(vector>& G, int v) { int low = S[v] = (int)S.size(); S.push_back(v); for(auto e : G[v]) if(at(e) < 0) low = min(low, S[e] ?: dfs(G, e)); if(low == S[v]) { comps.push_back({}); for(int i = S[v]; i < (int)S.size(); i++) { at(S[i]) = (int)comps.size() - 1; comps.back().push_back(S[i]); } S.resize(S[v]); } return low; } }; ``` We also need a ``vector`` to store the indegree for each SCC. ``` SCC scc(G); vector in((int)scc.comps.size()); ``` Iterate each node, if the ``i`` and ``j`` belong to different SCC, as they can be reachable each other, we increase the indegree of scc[j]. It is like making a SCC to a DAG. ``` for(int i = 0; i < N; i++) { for(auto j : G[i]) { if(scc[i] != scc[j]) { in[scc[j]]++; } } } ``` For those unreachable SCCs from the source SCC, their indegree must be 0. Hence, the answer is the number of those SCCs as we can add a path to each one to reach all the nodes within the SCC. ``` int ans = 0; for(int i = 0; i < (int)scc.comps.size(); i++) { ans += (in[i] == 0 && i != scc[S]); } cout << ans << endl; ```