Wednesday, 26 August 2020
Project Euler #001 - Multiples of 3 and 5
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3,5,6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below N.
Sample Input
```
2
10
100
```
Sample Output
```
23
2318
```
To sum from 1 to i, it is
```
s = 1 + 2 + 3... + (i - 1) + i
```
if you reverse the order
```
s = 1 + 2 + 3... + (i - 1) + i
s = i + (i - 1) + (i - 2) + ... + 2 + 1
```
summing each value, we got
```
2 * s = (i + 1) + (i + 1) + ...(i + 1) + (i + 1)
```
and there are ``i`` ``(i + 1)`` in above formula
```
2 * s = i * (i + 1)
```
at the end, we got
```
s = i * (i + 1) / 2
```
We can use ``s = i(i + 1) / 2`` to caculate the sum from 1 to ``i``. However, the question just needs us to calculate the sum of the multiples of 3 or 5.
Take 3 as an example
```
s = 3 + 6 + 9 + ... + 3i
s = 3(1 + 2 + 3 + ... + i)
```
We know that ``1 + 2 + 3 + ... + i`` can be calculated using ``s = i * (i + 1) / 2``. Therefore, we now know
```
s = 3 * (1 + 2 + 3 + ... + i)
s = 3 * (i * (i + 1) / 2)
```
where
```
3 * i <= n
i <= n / 3
```
it becomes
```
s = n * ((n / k)((n / k) + 1) / 2)
```
The question states that it only requires the multiples of K below N, that means it does not include N, hence we should substract N from 1.
However, if we sum up multiples of 3 and multiples of 5, we can get duplicate values, i.e. 15 in below example
```
multiples of 3: 3, 6, 9, 15, 18...
multiples of 5: 5, 10, 15, 20,...
```
Hence, we need to subtract the series of their least common multiple (LCM) which is 15. The final answer is
```
S(3) + S(5) - S(15)
```
Final Solution:
```cpp
ll t,i,x;
ll s(ll n,ll k){
x = n / k;
return (k * (x * (x + 1))) / 2;
}
int main()
{
FAST_INP;
cin >> t;
TC(t){
cin >> i;
cout << s(i - 1, 3) + s(i - 1, 5) - s(i - 1, 15) << "\n";
}
return 0;
}
```
Friday, 14 August 2020
Develop, release and operate Container Apps on AWS with the AWS Copilot CLI
Originally Copilot was called Amazon ECS CLI v2.
The AWS Copilot CLI is a tool for developers to create, release and manage production ready containerized applications on Amazon ECS and AWS Fargate. From getting started, pushing to a test environment and releasing to production, Copilot helps you through the entire life of your app development.
In short, you can develop, release and operate Container Apps on AWS with a few commands.
## Prerequisites
Before using Copilot, make sure you have installed AWS command line tool and setup your aws credentials. To do that, you can run ``aws configure`` to perform your setup. The region for this demonstration is ``ap-southeast-1``.
After the configuration setup, you can run the below command to verify
```bash
aws sts get-caller-identity
```
## Install
```
curl -Lo /usr/local/bin/copilot https://github.com/aws/copilot-cli/releases/download/v0.1.0/copilot-darwin-v0.1.0 &&
chmod +x /usr/local/bin/copilot &&
copilot --help
```
or through Homebrew
```
brew install aws/tap/copilot-cli
```
## Getting started
Run
```
copilot
```
to see the commands
```
👩✈️ Launch and manage applications on Amazon ECS and AWS Fargate.
Commands
Getting Started 🌱
init Create a new ECS application.
docs Open the copilot docs.
Develop ✨
app Commands for applications.
Applications are a collection of services and environments.
env Commands for environments.
Environments are deployment stages shared between services.
svc Commands for services.
Services are long-running Amazon ECS services.
Release 🚀
pipeline Commands for pipelines.
Continuous delivery pipelines to release services.
deploy Deploy your service.
Settings ⚙️
version Print the version number.
completion Output shell completion code.
Flags
-h, --help help for copilot
-v, --version version for copilot
Examples
Displays the help menu for the "init" command.
`$ copilot init --help`
```
## Init
Copilot will locate the Dockerfile automatically and ask you several questions. After that, it will create a new application containing your service(s).
A sample Dockerfile
```dockerfile
FROM nginx:alpine
EXPOSE 80
COPY . /usr/share/nginx/html
```
Run
```
copilot init
```
```
Application name: hello-world
Service type: Load Balanced Web Service
Service name: copilot-lb
Dockerfile: ./Dockerfile
Ok great, we'll set up a Load Balanced Web Service named copilot-lb in application hello-world listening on port 80.
✔ Created the infrastructure to manage services under application hello-world.
✔ Wrote the manifest for service copilot-lb at ../copilot-lb/manifest.yml
Your manifest contains configurations like your container size and port (:80).
✔ Created ECR repositories for service copilot-lb.
All right, you're all set for local development.
Deploy: Yes
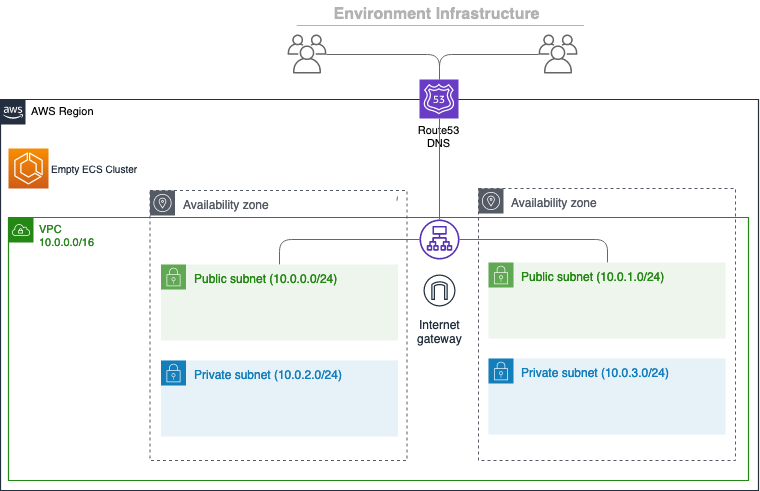
✔ Created the infrastructure for the test environment.
- Virtual private cloud on 2 availability zones to hold your services [Complete]
- Virtual private cloud on 2 availability zones to hold your services [Complete]
- Internet gateway to connect the network to the internet [Complete]
- Public subnets for internet facing services [Complete]
- Private subnets for services that can't be reached from the internet [Complete]
- Routing tables for services to talk with each other [Complete]
- ECS Cluster to hold your services [Complete]
- Application load balancer to distribute traffic [Complete]
✔ Linked account XXXXXXXXXXXX and region ap-southeast-1 to application hello-world.
```
You should be able to see the link at the end.
Click the link and verify that a simple nginx app is up and running
Go to ECS and you should see a cluster has been provisioned
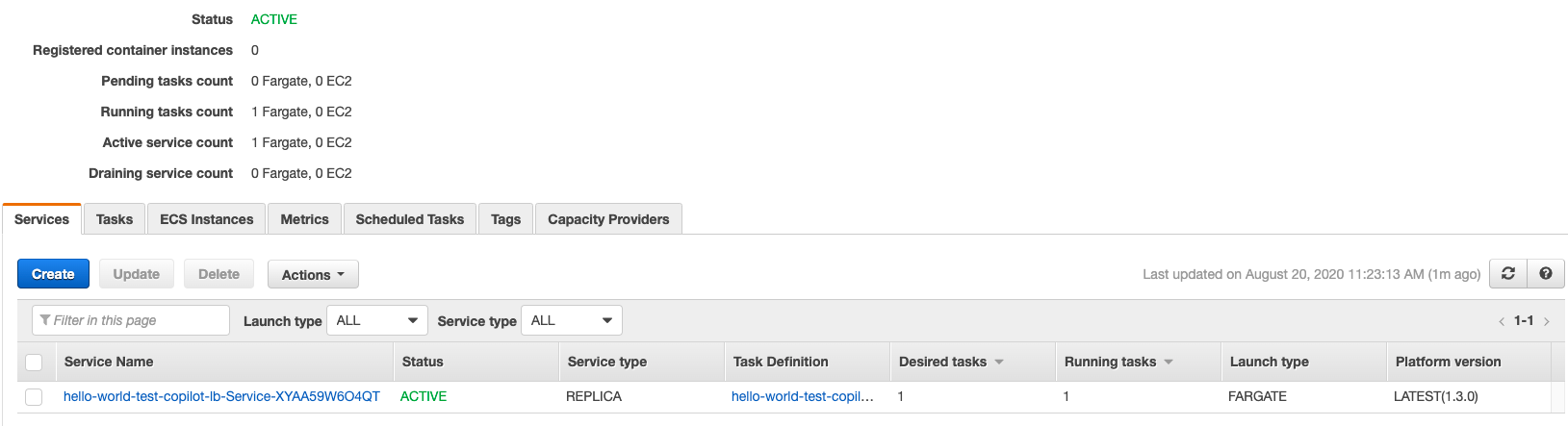
You can also take a look at ECS - Task Definition / ECR / EC2 - Load Balancer
## Logs
Copilot provides ``svc logs`` to allow users to check the service logs more easily. You can stream the logs or display the logs within a specfic timeslot
```
-a, --app string Name of the application.
--end-time string Optional. Only return logs before a specific date (RFC3339).
Defaults to all logs. Only one of end-time / follow may be used.
-e, --env string Name of the environment.
--follow Optional. Specifies if the logs should be streamed.
-h, --help help for logs
--json Optional. Outputs in JSON format.
--limit int Optional. The maximum number of log events returned. (default 10)
-n, --name string Name of the service.
--since duration Optional. Only return logs newer than a relative duration like 5s, 2m, or 3h.
Defaults to all logs. Only one of start-time / since may be used.
--start-time string Optional. Only return logs after a specific date (RFC3339).
Defaults to all logs. Only one of start-time / since may be used.
```
To stream the logs
```
copilot svc logs --follow
```
To display the logs within a specfic timeslot
```
copilot svc logs --start-time 2006-01-02T15:04:05+00:00 --end-time 2006-01-02T15:05:05+00:00
```
## Deploy
The application was deployed to the testing environment, which is a single small container to Fargate. It is only for development purposes.
To deploy in production, run the following command to create a new environment
```
copilot env init
```
Update the manifest file to tell Copilot the application is going to be deployed to production
```
environments:
production:
count: 2
cpu: 1024
memory: 2048
```
Copilot will create the infrastructure fro the production environment
```
What is your environment's name? prod
Which named profile should we use to create prod? default
✔ Created the infrastructure for the prod environment.
- Virtual private cloud on 2 availability zones to hold your services [Complete]
- Virtual private cloud on 2 availability zones to hold your services [Complete]
- Internet gateway to connect the network to the internet [Complete]
- Public subnets for internet facing services [Complete]
- Private subnets for services that can't be reached from the internet [Complete]
- Routing tables for services to talk with each other [Complete]
- ECS Cluster to hold your services [Complete]
- Application load balancer to distribute traffic [Complete]
✔ Linked account XXXXXXXXXXXX and region ap-southeast-1 to application hello-world.
✔ Created environment prod in region ap-southeast-1 under application hello-world.
```
Deploy your service to production
```
copilot svc deploy --env production
```
## Clean up
```
copilot env list
```
I got
```
test
prod
```
Force delete the application with environments "test" and "prod"
```
copilot app delete --yes --env-profiles test=default,prod=prod-profile
```
## Conclusion
Copilot can help you to deploy your service containerized to production with a few commands. What you need is just Copilot and Dockerfile.
Copilot is still in beta. Some services like provisioning storage are not supported yet. (As of 20/08/2020)
## For more
- https://github.com/aws/copilot-cli
Monday, 10 August 2020
Getting Started with Azure Databricks
## Sample Cluster Setup
```json
{
"num_workers": 5,
"cluster_name": "Databricks-playground",
"spark_version": "6.5.x-scala2.11",
"spark_conf": {
"spark.dynamicAllocation.enabled": "true",
"spark.shuffle.compress": "true",
"spark.shuffle.spill.compress": "true",
"spark.executor.memory": "7849M",
"spark.sql.shuffle.partitions": "1024",
"spark.network.timeout": "600s",
"spark.executor.instances": "0",
"spark.driver.memory": "7849M",
"spark.dynamicAllocation.executorIdleTimeout": "600s"
},
"node_type_id": "Standard_F8s",
"driver_node_type_id": "Standard_F8s",
"ssh_public_keys": [],
"custom_tags": {},
"cluster_log_conf": {
"dbfs": {
"destination": "dbfs:/cluster-logs"
}
},
"spark_env_vars": {
"PYSPARK_PYTHON": "/databricks/python3/bin/python3"
},
"autotermination_minutes": 0,
"init_scripts": []
}
```
## Common commands
List the directory in DBFS
```
%fs ls
```
Create a directory in DBFS
```
%fs mkdirs src
```
Copy files from src to dist in DBFS
```
%fs cp -r dbfs:/src dbfs:/dist
```
## Setup Mount Point for Blob Storage
Using an old driver called WASB
### Create Secret Scope
By default, scopes are created with MANAGE permission for the user who created the scope. If your account does not have the Premium plan (or, for customers who subscribed to Databricks before March 3, 2020, the Operational Security package), you must override that default and explicitly grant the MANAGE permission to “users” (all users) when you create the scope
```
databricks secrets create-scope --scope --initial-manage-principal users
```
To verify
```
databricks secrets list-scopes
```
### Create Secret
```
databricks secrets put --scope --key --string-value
```
The value of can be retrieved from Storage Account -> Settings -> Access Keys
### Create Mount Point
```python
dbutils.fs.mount(
source = "wasbs://@.blob.core.windows.net",
mount_point = "/mnt/",
extra_configs = {"":dbutils.secrets.get(scope = "", key = "")}
)
```
To verify in Databricks Notebook
```python
%fs dbfs:/mnt/
```
## Setup Mount Point for ADLS Gen 2
Requiring the following items
- ``application-id``: An ID that uniquely identifies the application.
- ``directory-id``: An ID that uniquely identifies the Azure AD instance.
- ``storage-account-name``: The name of the storage account.
- ``service-credential``: A string that the application uses to prove its identity.
### Create Mount Point
```python
configs = {"fs.azure.account.auth.type": "OAuth",
"fs.azure.account.oauth.provider.type": "org.apache.hadoop.fs.azurebfs.oauth2.ClientCredsTokenProvider",
"fs.azure.account.oauth2.client.id": "",
"fs.azure.account.oauth2.client.secret": dbutils.secrets.get(scope="",key=""),
"fs.azure.account.oauth2.client.endpoint": "https://login.microsoftonline.com//oauth2/token"}
# Optionally, you can add to the source URI of your mount point.
dbutils.fs.mount(
source = "abfss://@.dfs.core.windows.net/",
mount_point = "/mnt/",
extra_configs = configs)
```
## Performance Tuning
- Use Ganglia to see the metrics and gain insights
- Use Spark 3.0 if your application contians lots of joining logic
- Adaptive Query Execution to speed up Spark SQL at runtime
- Ref: https://databricks.com/blog/2020/05/29/adaptive-query-execution-speeding-up-spark-sql-at-runtime.html
- Simply enable it by setting ``spark.sql.adaptive.enabled`` to ``true``
## Common issues
### No output files written in storage
Probably it is out of memory. Try adjust the hardware settings.
### Clusters settings not apply to jobs
Make sure the cluster is interactive or automated. Interactive one is for notebooks. If you create a job, you should be able to modify the cluster settings in the job creation page.
### Spark conf is not supported via cluster settings for spark-submit task
Self-explanatory
```
{"error_code":"INVALID_PARAMETER_VALUE","message":"Spark conf is not supported via cluster settings for spark-submit task. Please use spark-submit parameters to set spark conf."}
```
### Custom Dependencies cannot be found
Suppose your package is located in ``/dbfs/databricks/driver/jobs/``, add the following code in your entry point.
Python Example:
```python
import sys
sys.path.append("/dbfs/databricks/driver/jobs/")
```
## References:
- [Databricks File System (DBFS)](https://docs.databricks.com/data/databricks-file-system.html)
- [Create a Databricks-backed secret scope](https://docs.databricks.com/security/secrets/secret-scopes.html)
- [Azure Data Lake Storage Gen2](https://docs.microsoft.com/en-us/azure/databricks/data/data-sources/azure/azure-datalake-gen2)
Subscribe to:
Posts (Atom)